
【題目】如圖,已知![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
且![]() 是
是![]() 的中點,
的中點,![]() .
.
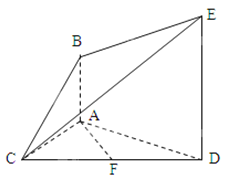
(1)求證:![]() 平面
平面![]() ;
;
(2)求證:平面![]() 平面
平面![]() ;
;
(3)求此多面體的體積.
【答案】(1)詳見解析;(2)詳見解析;(3)![]() .
.
【解析】
試題(1)取![]() 中點
中點![]() ,連接
,連接![]() 、
、![]() ,結合三角形中位線定理,可得
,結合三角形中位線定理,可得![]() ,且
,且![]() ,進而得到
,進而得到![]() ,結合線面平行的判定定理,即可得到
,結合線面平行的判定定理,即可得到![]() 平面
平面![]() ;(2)首先判斷
;(2)首先判斷![]() 為正三角形,結合
為正三角形,結合![]() 為中點可得
為中點可得![]() ,又由已知可得
,又由已知可得![]() ,根據線面垂直的判定定理,可得
,根據線面垂直的判定定理,可得![]() 平面
平面![]() ,進而根據面面平行的判定定理,得到平面
,進而根據面面平行的判定定理,得到平面![]() 平面
平面![]() ;(3)多面體是以
;(3)多面體是以![]() 為頂點,以四邊形
為頂點,以四邊形![]() 為底邊的四棱錐,求出棱錐的高及底面面積,然后代入棱錐的體積公式,即可求出答案.
為底邊的四棱錐,求出棱錐的高及底面面積,然后代入棱錐的體積公式,即可求出答案.
試題解析:(1)取![]() 中點
中點![]() ,連結
,連結![]() 、
、![]() ,
,![]() 為
為![]() 的中點,
的中點, ,且
![]() ,又
,又![]() ,且
,且![]()
![]() ,且
,且![]() ,
,![]() 為平行四邊形,
為平行四邊形,![]() , 又
, 又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)![]() ,
,![]() ,所以
,所以![]() 為正三角形,
為正三角形,![]() ,
,
![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
![]() ,又
,又![]() ,
,![]() ,
,![]() 平面
平面![]() ,又
,又![]() ,
,![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() ;
;
(3)此多面體是一個以![]() 為定點,以四邊形
為定點,以四邊形![]() 為底邊的四棱錐,
為底邊的四棱錐,
![]() ,平面
,平面![]() 平面
平面![]() ,
,
![]() 等邊三角形
等邊三角形![]() 邊上的高就是四棱錐的高,
邊上的高就是四棱錐的高,![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】以下兩個圖表是2019年初的4個月我國四大城市的居民消費價格指數(上一年同月![]() )變化圖表,則以下說法錯誤的是( )
)變化圖表,則以下說法錯誤的是( )
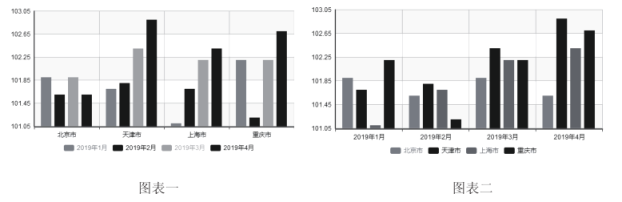
(注:圖表一每個城市的條形圖從左到右依次是1、2、3、4月份;圖表二每個月份的條形圖從左到右四個城市依次是北京、天津、上海、重慶)
A.3月份四個城市之間的居民消費價格指數與其它月份相比增長幅度較為平均
B.4月份僅有三個城市居民消費價格指數超過102
C.四個月的數據顯示北京市的居民消費價格指數增長幅度波動較小
D.僅有天津市從年初開始居民消費價格指數的增長呈上升趨勢
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩個定點![]() ,動點
,動點![]() 滿足
滿足![]() .設動點
.設動點![]() 的軌跡為曲線
的軌跡為曲線![]() ,直線
,直線![]() .
.
(1)求曲線![]() 的軌跡方程;
的軌跡方程;
(2)若![]() 與曲線
與曲線![]() 交于不同的
交于不同的![]() 兩點,且
兩點,且![]() (
(![]() 為坐標原點),求直線
為坐標原點),求直線![]() 的斜率;
的斜率;
(3)若![]() ,
, ![]() 是直線
是直線![]() 上的動點,過
上的動點,過![]() 作曲線
作曲線![]() 的兩條切線
的兩條切線![]() ,切點為
,切點為![]() ,探究:直線
,探究:直線![]() 是否過定點.
是否過定點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在《九章算術》中,將四個面都為直角三角形的四面體稱之為鱉臑.如圖,在鱉臑![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,且
,且![]() ,過點
,過點![]() 分別作
分別作![]() 于點
于點![]() ,
,![]() 于點
于點![]() ,連結
,連結![]() ,當
,當![]() 的面積最大時,
的面積最大時,![]() __________.
__________.
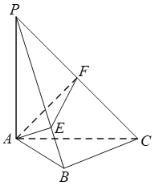
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車的投放,方便了市民短途出行,被譽為中國“新四大發明”之一.某市為研究單車用戶與年齡的相關程度,隨機調查了100位成人市民,統計數據如下:
不小于40歲 | 小于40歲 | 合計 | |
單車用戶 | 12 | 18 | 30 |
非單車用戶 | 38 | 32 | 70 |
合計 | 50 | 50 | 100 |
(1)從獨立性檢驗角度分析,能否有![]() 以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關;
以上的把握認為該市成人市民是否為單車用戶與年齡是否小于40歲有關;
(2)將此樣本的頻率做為概率,從該市單車用戶中隨機抽取3人,記不小于40歲的單車用戶的人數為![]() ,求
,求![]() 的分布列與數學期望.
的分布列與數學期望.
下面臨界值表供參考:
P( | 0.15 | 0.10 | 0.05 | 0.25 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(參考公式: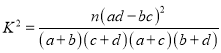 ,其中
,其中![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】材料一:2018年,全國逾半省份將從秋季入學的高一年級開始實行新的學業水平考試和高考制度.所有省級行政區域均突破文理界限,由學生跨文理選科,均設 置“![]() ”的考試科目.前一個“3”為必考科目,為統一高考科目語文、數學、外語.除個別省級行政區域仍執行教育部委托的分省命題任務外,絕大部分省級行政區域均由教育部考試中心統一命題;后一個“3”為高中學業水平考試(簡稱“學考”)選考科目,由各省級行政區域自主命題.材料二:2019年4月,河北、遼寧、江蘇、福建、湖北、湖南、廣東、重慶等8省市發布高考綜合改革實施方案,方案決定從2018年秋季入學的高中一年級學生開始實施高考綜合改革.考生總成績由全國統一高考的語文、數學、外語3個科目成績和考生選擇的3科普通高中學業水平選擇性考試科目成績組成,滿分為750分.即通常所說的“
”的考試科目.前一個“3”為必考科目,為統一高考科目語文、數學、外語.除個別省級行政區域仍執行教育部委托的分省命題任務外,絕大部分省級行政區域均由教育部考試中心統一命題;后一個“3”為高中學業水平考試(簡稱“學考”)選考科目,由各省級行政區域自主命題.材料二:2019年4月,河北、遼寧、江蘇、福建、湖北、湖南、廣東、重慶等8省市發布高考綜合改革實施方案,方案決定從2018年秋季入學的高中一年級學生開始實施高考綜合改革.考生總成績由全國統一高考的語文、數學、外語3個科目成績和考生選擇的3科普通高中學業水平選擇性考試科目成績組成,滿分為750分.即通常所說的“![]() ”模式,所謂“
”模式,所謂“![]() ”,即“3”是三門主科,分別是語文、數學、外語,這三門科目是必選的.“1”指的是要在物理、歷史里選一門,按原始分計入成績.“2”指考生要在生物、化學、思想政治、地理4門中選擇2門.但是這幾門科目不以原始分計入成績,而是等級賦分.等級賦分指的是把考生的原始成績根據人數的比例分為
”,即“3”是三門主科,分別是語文、數學、外語,這三門科目是必選的.“1”指的是要在物理、歷史里選一門,按原始分計入成績.“2”指考生要在生物、化學、思想政治、地理4門中選擇2門.但是這幾門科目不以原始分計入成績,而是等級賦分.等級賦分指的是把考生的原始成績根據人數的比例分為![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個等級,五個等級分別對應著相應的分數區間,然后再用公式換算,轉換得出分數.
五個等級,五個等級分別對應著相應的分數區間,然后再用公式換算,轉換得出分數.
(1)若按照“![]() ”模式選科,求選出的六科中含有“語文,數學,外語,物理,化學”的概率.
”模式選科,求選出的六科中含有“語文,數學,外語,物理,化學”的概率.
(2)某教育部門為了調查學生語數外三科成績與選科之間的關系,現從當地不同層次的學校中抽取高一學生2500名參加語數外的網絡測試,滿分450分,并給前400名頒發榮譽證書,假設該次網絡測試成績服從正態分布,且滿分為450分;
①考生甲得知他的成績為270分,考試后不久了解到如下情況:“此次測試平均成績為171分,351分以上共有57人”,問甲能否獲得榮譽證書,請說明理由;
②考生丙得知他的實際成績為430分,而考生乙告訴考生丙:“這次測試平均成績為201分,351分以上共有57人”,請結合統計學知識幫助丙同學辨別乙同學 信息的真偽.
附:![]() ;
;![]() ;
;![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() ,
,![]() 平面
平面![]() ,底面
,底面![]() 為正方形,且
為正方形,且![]() .若四棱錐
.若四棱錐![]() 的每個頂點都在球
的每個頂點都在球![]() 的球面上,則球
的球面上,則球![]() 的表面積的最小值為_____;當四棱錐
的表面積的最小值為_____;當四棱錐![]() 的體積取得最大值時,二面角
的體積取得最大值時,二面角![]() 的正切值為_______.
的正切值為_______.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com