
【題目】如圖所示,在幾何體![]() 中,
中,![]() 是等邊三角形,
是等邊三角形,![]() 平面
平面![]() ,
,![]() ,且
,且![]() .
.
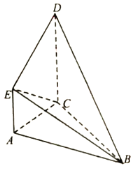
(I)試在線段![]() 上確定點
上確定點![]() 的位置,使
的位置,使![]() 平面
平面![]() ,并證明;
,并證明;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(I)見解析;(II)![]()
【解析】
(I)取![]() 為
為![]() 的中點,連接EM,取
的中點,連接EM,取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,證明四邊形
,證明四邊形![]() 為平行四邊形,得
為平行四邊形,得![]() 再證明
再證明![]() 平面
平面![]() 即可證明
即可證明![]() 平面
平面![]() ,則M為所求;(II)以
,則M為所求;(II)以![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 所在的直線分別為
所在的直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系,求平面
軸,建立如圖所示的空間直角坐標系,求平面![]() 和平面
和平面![]() 的法向量,利用二面角的向量公式求解即可
的法向量,利用二面角的向量公式求解即可
(I)當點![]() 為
為![]() 的中點時,
的中點時,![]() 平面
平面![]() .證明如下:取
.證明如下:取![]() 中點
中點![]() ,連接
,連接![]() ,
,![]() ,
,
![]() 且
且![]() ,又
,又![]() ,
,![]() ,
,
![]() 且
且![]() ,
,![]() 四邊形
四邊形![]() 為平行四邊形,
為平行四邊形,![]() .
.
又![]() 平面
平面![]() ,
,![]() ,
,![]() 平面
平面![]() ,又CD
,又CD![]() 面BCD,
面BCD,![]() 平面
平面![]() 平面
平面![]() ,
,![]() 是等邊三角形,
是等邊三角形,![]() ,
,
又平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() .
.
(II)由(I)FA,FB,FM兩兩互相垂直,以![]() 為原點,以
為原點,以![]() ,
,![]() ,
,![]() 所在的直線分別為
所在的直線分別為![]() 軸,
軸,![]() 軸,
軸,![]() 軸,建立如圖所示的空間直角坐標系,設
軸,建立如圖所示的空間直角坐標系,設![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() .設平面
.設平面![]() 的法向量為
的法向量為![]() ,
,
則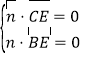 ,即
,即![]() ,解得
,解得![]() ,
,
令![]() ,則
,則![]() ,
,![]() ,由(I)知,平面
,由(I)知,平面![]() 的一個法向量為
的一個法向量為![]() ,
,
![]() ,
,![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.



 考前必練系列答案
考前必練系列答案科目:高中數學 來源: 題型:
【題目】如圖,在三棱錐![]() 中,
中,![]() 與
與![]() 都為等邊三角形,且側面
都為等邊三角形,且側面![]() 與底面
與底面![]() 互相垂直,
互相垂直,![]() 為
為![]() 的中點,點
的中點,點![]() 在線段
在線段![]() 上,且
上,且![]() ,
,![]() 為棱
為棱![]() 上一點.
上一點.
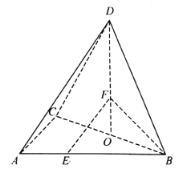
(1)試確定點![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)在(1)的條件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面四邊形![]() 中(圖1),
中(圖1),![]() 為
為![]() 的中點,
的中點,![]() ,且
,且![]() ,現將此平面四邊形沿
,現將此平面四邊形沿![]() 折起,使得二面角
折起,使得二面角![]() 為直二面角,得到一個多面體,
為直二面角,得到一個多面體,![]() 為平面
為平面![]() 內一點,且
內一點,且![]() 為正方形(圖2),
為正方形(圖2),![]() 分別為
分別為![]() 的中點.
的中點.
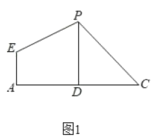
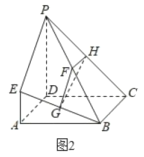
(1)求證:平面![]() //平面
//平面![]() ;
;
(2)在線段![]() 上是否存在一點
上是否存在一點![]() ,使得平面
,使得平面![]() 與平面
與平面![]() 所成二面角的余弦值為
所成二面角的余弦值為![]() ?若存在,求出線段
?若存在,求出線段![]() 的長,若不存在,請說明理由.
的長,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.該原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖,在空間直角坐標系中的![]() 平面內,若函數
平面內,若函數![]() 的圖象與
的圖象與![]() 軸圍成一個封閉的區域
軸圍成一個封閉的區域![]() ,將區域
,將區域![]() 沿
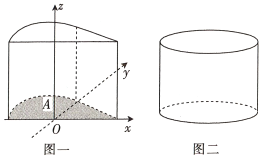
沿![]() 軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域
軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域![]() 的面積相等,則此圓柱的體積為__________.
的面積相等,則此圓柱的體積為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.該原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖,在空間直角坐標系中的![]() 平面內,若函數
平面內,若函數![]() 的圖象與
的圖象與![]() 軸圍成一個封閉的區域
軸圍成一個封閉的區域![]() ,將區域
,將區域![]() 沿
沿![]() 軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域
軸的正方向平移8個單位長度,得到幾何體如圖一,現有一個與之等高的圓柱如圖二,其底面積與區域![]() 的面積相等,則此圓柱的體積為__________.
的面積相等,則此圓柱的體積為__________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知斜率為1的直線![]() 與橢圓
與橢圓![]() 交于
交于![]() ,
,![]() 兩點,且線段
兩點,且線段![]() 的中點為
的中點為![]() ,橢圓
,橢圓![]() 的上頂點為
的上頂點為![]() .
.
(1)求橢圓![]() 的離心率;
的離心率;
(2)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,若直線
兩點,若直線![]() 與
與![]() 的斜率之和為2,證明:
的斜率之和為2,證明:![]() 過定點.
過定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com