
分析 (Ⅰ)由正弦定理、兩角和的正弦公式化簡已知的條件,求出cosA的值,由A的范圍和特殊角的三角函數值求出角A的值;
(Ⅱ)由條件和正弦定理求出sin∠ADB,由條件求出∠ADB,由內角和定理分別求出∠ABC、∠ACB,結合條件和余弦定理求出邊a的值.
解答 解:(Ⅰ)由2acosC-c=2b及正弦定理得,
2sinAcosC-sinC=2sinB,…(2分)
2sinAcosC-sinC=2sin(A+C)=2sinAcosC+2cosAsinC,
∴-sinC=2cosAsinC,
∵sinC≠0,∴cosA=$-\frac{1}{2}$,
又A∈(0,π),∴A=$\frac{2π}{3}$;…(6分)
(Ⅱ)在△ABD中,c=$\sqrt{2}$,角B的平分線BD=$\sqrt{3}$,
由正弦定理得$\frac{AB}{sin∠ADB}=\frac{BD}{sinA}$,
∴sin∠ADB=$\frac{ABsinA}{BD}$=$\frac{\sqrt{2}×\frac{\sqrt{3}}{2}}{\sqrt{3}}$=$\frac{\sqrt{2}}{2}$,…(8分)
由A=$\frac{2π}{3}$得∠ADB=$\frac{π}{4}$,∴∠ABC=2($π-\frac{2π}{3}-\frac{π}{4}$)=$\frac{π}{6}$,
∴∠ACB=$π-\frac{2π}{3}-\frac{π}{6}$=$\frac{π}{6}$,AC=AB=$\sqrt{2}$
由余弦定理得,a2=BC2═AB2+AC2-2AB•AC•cosA
=2+2-2×$\sqrt{2}×\sqrt{2}×(-\frac{1}{2})$=6,
∴a=$\sqrt{6}$…(12分)
點評 本題考查正弦定理、余弦定理,內角和定理,以及兩角和的正弦公式等應用,考查轉化思想,化簡、變形能力.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{7}{4}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | {x|-1<x<$\frac{3}{2}$} | B. | {x|x>$\frac{3}{2}$或x<-1} | C. | {x|-$\frac{3}{2}$<x<1} | D. | {x|x>1或x<-$\frac{3}{2}$} |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
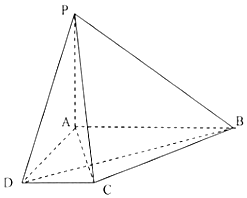 如圖,四棱錐P-ABCD中,底面ABCD為直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.
如圖,四棱錐P-ABCD中,底面ABCD為直角梯形,∠BAD=∠ADC=90°,AP=AD=2CD=1,AB=2,PA⊥平面ABCD.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (1,$\sqrt{3}$) | B. | ($\sqrt{3}$,+∞) | C. | (0,$\sqrt{3}$) | D. | (2,$\sqrt{3}$) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
| 時間(t) | 2 | 4 | 6 | 8 | 10 |
| 日銷售量(y) | 38 | 37 | 32 | 33 | 30 |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com