
【題目】如圖1,在平行四邊形![]() 中,
中,![]() ,
,![]() ,
,![]() ,以對角線
,以對角線![]() 為折痕把
為折痕把![]() 折起,使點
折起,使點![]() 到圖2所示點
到圖2所示點![]() 的位置,使得
的位置,使得![]() .
.
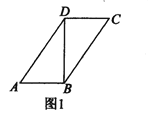

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(Ⅰ)見解析; (Ⅱ)![]() .
.
【解析】
(Ⅰ)在圖1中,求解三角形可得AB⊥BD,同理CD⊥BD,圖2中,在△PAD中,求解三角形可得AD⊥PD,結合PD⊥BD,得到PD⊥平面ABD,進一步得到PD⊥AB,
又AB⊥BD,可得AB⊥平面PBD,由面面垂直的判定可得平面PAB⊥平面PBD;
(Ⅱ)以D為坐標原點,分別以DB,DP所在直線為y,z軸,過點D在平面ABD內平行于AB的直線為x軸建立空間直角坐標系,分別求出平面PAD與平面PAB的一個法向量,由兩法向量所成角的余弦值可得二面角B-PA-D的余弦值.
(Ⅰ)圖1中,![]() ,
,
由余弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,
,
即![]() ,
,
同理![]() .
.
圖2中,在![]() 中,
中,![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
又![]() ,∴
,∴![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,∴
,∴![]() ,
,
又![]() .∴
.∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)如圖,以![]() 為坐標原點,
為坐標原點,![]() 所在直線分別為
所在直線分別為![]() 軸,
軸,
過點![]() 在平面
在平面![]() 內平行于
內平行于![]() 的直線為
的直線為![]() 軸建立空間直角坐標系.
軸建立空間直角坐標系.
則![]() ,
,![]()
設平面![]() 的法向量為
的法向量為![]()
由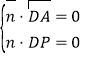 得
得![]() 令
令![]() ,得平面
,得平面![]() 的一個法向量為
的一個法向量為![]()
同理可得平面![]() 的一個法向量
的一個法向量![]()
∴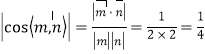 .
.
又二面角![]() 的平面角為銳角,
的平面角為銳角,
所以,二面角![]() 的余弦值為
的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據表格提供的數據求函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 周期為
周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.回歸直線![]() 至少經過其樣本數據
至少經過其樣本數據![]() 中的一個點
中的一個點
B.從獨立性檢驗可知有99%的把握認為吃地溝油與患胃腸癌有關系時,我們就說如果某人吃地溝油,那么他有99%可能患胃腸癌
C.在殘差圖中,殘差點分布的帶狀區域的寬度越狹窄,其模型擬合的精度越高
D.將一組數據的每一個數據都加上或減去同一個常數后,其方差也要加上或減去這個常數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,曲線C1的極坐標方程是![]() ,在以極點為原點O,極軸為x軸正半軸(兩坐標系取相同的單位長度)的直角坐標系xOy中,曲線C2的參數方程為
,在以極點為原點O,極軸為x軸正半軸(兩坐標系取相同的單位長度)的直角坐標系xOy中,曲線C2的參數方程為![]() (θ為參數).
(θ為參數).
(1)求曲線C1的直角坐標方程與曲線C2的普通方程;
(2)將曲線C2經過伸縮變換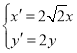 后得到曲線C3,若M,N分別是曲線C1和曲線C3上的動點,求|MN|的最小值.
后得到曲線C3,若M,N分別是曲線C1和曲線C3上的動點,求|MN|的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某年級![]() 位同學參加語文和數學兩門課的考試,每門課的考分從0到100分. 假如考試的結果沒有兩位同學的成績是完全相同的(即至少有一門課的成績不同). 另外,“甲比乙好”是指同學甲的語文和數學的考分均分別高于同學乙的語文和數學的考分. 試問:當
位同學參加語文和數學兩門課的考試,每門課的考分從0到100分. 假如考試的結果沒有兩位同學的成績是完全相同的(即至少有一門課的成績不同). 另外,“甲比乙好”是指同學甲的語文和數學的考分均分別高于同學乙的語文和數學的考分. 試問:當![]() 最小為何值時,必存在三位同學(設為甲、乙、丙),有甲比乙好,乙比丙好.
最小為何值時,必存在三位同學(設為甲、乙、丙),有甲比乙好,乙比丙好.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的焦距為8,其短軸的兩個端點與長軸的一個端點構成正三角形。
的焦距為8,其短軸的兩個端點與長軸的一個端點構成正三角形。
(1)求![]() 的方程;
的方程;
(2)設![]() 為
為![]() 的左焦點,
的左焦點,![]() 為直線
為直線![]() 上任意一點,過點
上任意一點,過點![]() 作
作![]() 的垂線交
的垂線交![]() 于兩點
于兩點![]() ,
,![]() .
.
(i)證明:![]() 平分線段
平分線段![]() (其中
(其中![]() 為坐標原點);
為坐標原點);
(ii)當![]() 取最小值時,求點
取最小值時,求點![]() 的坐標。
的坐標。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣x2+ax,g(x)=ex﹣e,其中a>0.
(1)若a=1,證明:f(x)≤0;
(2)用max{m,n}表示m和n中的較大值,設函數h(x)=max{f(x),g(x)},討論函數h(x)在(0,+∞)上的零點的個數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com