
【題目】已知函數![]() 的一系列對應值如下表:
的一系列對應值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)根據表格提供的數據求函數![]() 的一個解析式;
的一個解析式;
(2)根據(1)的結果,若函數![]() 周期為
周期為![]() ,當
,當![]() 時,方程
時,方程![]() 恰有兩個不同的解,求實數
恰有兩個不同的解,求實數![]() 的取值范圍.
的取值范圍.
 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:高中數學 來源: 題型:
【題目】(2018·邯鄲一模)若甲、乙兩類水果的質量(單位:kg)分別服從正態分布N(μ1,σ2)及N(μ2,σ2),其正態分布的密度曲線如圖所示,則下列說法錯誤的是( )

A. 乙類水果的質量服從的正態分布的參數σ2=64
B. 甲類水果的質量比乙類水果的質量更集中
C. 甲類水果的平均質量μ1=0.4 kg
D. 甲類水果的平均質量比乙類水果的平均質量小
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】搶“微信紅包”已經成為中國百姓歡度春節時非常喜愛的一項活動.小明收集班內20名同學今年春節期間搶到紅包金額![]() (元)如下(四舍五入取整數):
(元)如下(四舍五入取整數):
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
對這20個數據進行分組,各組的頻數如下:
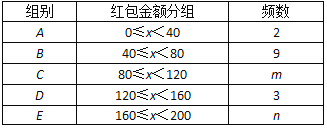
(Ⅰ)寫出m,n的值,并回答這20名同學搶到的紅包金額的中位數落在哪個組別;
(Ⅱ)記C組紅包金額的平均數與方差分別為![]() 、
、![]() ,E組紅包金額的平均數與方差分別為
,E組紅包金額的平均數與方差分別為![]() 、
、![]() ,試分別比較
,試分別比較![]() 與
與![]() 、
、![]() 與
與![]() 的大小;(只需寫出結論)
的大小;(只需寫出結論)
(Ⅲ)從A,E兩組所有數據中任取2個,求這2個數據差的絕對值大于100的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某研究所計劃利用“神舟十一號”飛船進行新產品搭載實驗,計劃搭載新產品![]() ,要根據該產品的研制成本、產品質量、搭載實驗費用和預計產生收益來決定具體安排,通過調查,搭載每件產品有關數據如表:
,要根據該產品的研制成本、產品質量、搭載實驗費用和預計產生收益來決定具體安排,通過調查,搭載每件產品有關數據如表:
因素 | 產品 | 產品 | 備注 |
研制成本、搭載費用之和/萬元 | 20 | 30 | 計劃最大投資 |
金額300萬元產品質量/千克 | 10 | 5 | 最大搭載 |
質量110千克預計收益/萬元 | 80 | 60 | —— |
則使總預計收益達到最大時, ![]() 兩種產品的搭載件數分別為( )
兩種產品的搭載件數分別為( )
A. 9,4 B. 8,5 C. 9,5 D. 8,4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】研究發現,北京 PM 2.5 的重要來源有土壤塵、燃煤、生物質燃燒、汽車尾氣與垃圾焚燒、工業污染和二次無機氣溶膠,其中燃煤的平均貢獻占比約為 18%.為實現“節能減排”,還人民“碧水藍天”,北京市推行“煤改電”工程,采用空氣源熱泵作為冬天供暖.進入冬季以來,該市居民用電量逐漸增加,為保證居民取暖,市供電部門對該市 100 戶居民冬季(按 120 天計算)取暖用電量(單位:度)進行統計分析,得到居民冬季取暖用電量的頻率分布直方圖如圖所示.

(1)求頻率分布直方圖中![]() 的值;
的值;
(2)從這 100 戶居民中隨機抽取 1 戶進行深度調查,求這戶居民冬季取暖用電量在[3300,3400]的概率;
(3)在用電量為[3200,3250),[3250,3300),[3300,3350),[3350,3400]的四組居民中,用分層抽樣的方法抽取 34 戶居民進行調查,則應從用電量在[3200,3250)的居民中抽取多少戶?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分16分)
已知數列{an}的前n項和為Sn,且a1=1,Sn=n2an(n∈N*).
(1)試求出S1,S2,S3,S4,并猜想Sn的表達式;
(2)用數學納法證明你的猜想,并求出an的表達式.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(數學文卷·2017屆湖北省黃岡市高三上學期期末考試第16題) “中國剩余定理”又稱“孫子定理”.1852年英國來華傳教偉烈亞利將《孫子算經》中“物不知數”問題的解法傳至歐洲.1874年,英國數學家馬西森指出此法符合1801年由高斯得出的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”. “中國剩余定理”講的是一個關于整除的問題,現有這樣一個整除問題:將2至2017這2016個數中能被3除余1且被5除余1的數按由小到大的順序排成一列,構成數列![]() ,則此數列的項數為__________.
,則此數列的項數為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com