
【題目】已知函數f(x)=lnx﹣x2+ax,g(x)=ex﹣e,其中a>0.
(1)若a=1,證明:f(x)≤0;
(2)用max{m,n}表示m和n中的較大值,設函數h(x)=max{f(x),g(x)},討論函數h(x)在(0,+∞)上的零點的個數.
【答案】(1)證明見解析;(2)當0<a≤1時,h(x)在(0,+∞)上有唯一的零點;當a>1時,h(x)在(0,+∞)上也有1個零點
【解析】
(1)對f(x)求導,然后求出f'(x)的零點,再判斷f(x)的單調性,然后求出f(x)的最大值,進而證明f(x)≤0成立;
(2)由條件知h(x)在區間(1,+∞)上不可能有零點,然后根據條件考慮在區間(0,1)上和x=1處時h(x)的零點情況即可.
解:(1)![]() (x>0),
(x>0),
令f'(x)=0,則x=1或![]() (舍),
(舍),
∴當x∈(0,1)時,![]() >0,f(x)單調遞增,
>0,f(x)單調遞增,
當x∈(1,+∞)時,![]() <0,f(x)單調遞減,
<0,f(x)單調遞減,
∴f(x)≤f(x)max=f(1)=0.
(2)![]() 是
是![]() 上的增函數,
上的增函數,![]() ,
,
在區間(1,+∞)上,g(x)>0,∴h(x)=max{f(x),g(x)}≥g(x)>0,
∴h(x)在區間(1,+∞)上不可能有零點.
下面只考慮區間(0,1)上和x=1處的情況.
由題意f(x)的定義域為(0,+∞),![]() .
.
令![]() =0可得
=0可得![]() (負值舍去).
(負值舍去).
在(0,x0)上![]() >0,f(x)為增函數,在(x0,+∞)上
>0,f(x)為增函數,在(x0,+∞)上![]() <0,f(x)為減函數,
<0,f(x)為減函數,
∴f(x)max=f(x0).
①當a=1時,x0=1,∴f(x)max=f(1)=0.
∵在區間(0,1)上,g(x)<0,且g(1)=0,
∴此時h(x)存在唯一的零點x=1.
②當0<a<1時,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴ ,
,
于是f(x)<0恒成立,結合函數g(x)的性質,
可知此時h(x)存在唯一的零點x=1.
③當a>1時,![]() ,∴f(x)在(0,1)上遞增.
,∴f(x)在(0,1)上遞增.
又∵f(1)=a﹣1>0,![]() ,
,
∴f(x)在區間(0,1)上存在唯一的零點x=x1.
結合函數g(x)的性質,可知x=x1是h(x)唯一的零點.
綜上,當0<a≤1時,h(x)在(0,+∞)上有唯一的零點x=1;
當a>1時,h(x)在(0,+∞)上也有1個零點.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】《中國詩詞大會》(第三季)亮點頗多,在“人生自有詩意”的主題下,十場比賽每場都有一首特別設計的開場詩詞在聲光舞美的配合下,百人團齊聲朗誦,別有韻味.若《沁園春·長沙》、《蜀道難》、《敕勒歌》、《游子吟》、《關山月》、《清平樂·六盤山》排在后六場,且《蜀道難》排在《游子吟》的前面,《沁園春·長沙》與《清平樂·六盤山》不相鄰且均不排在最后,則后六場的排法有__________種.(用數字作答)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 點為圓
點為圓![]() 上的動點,點
上的動點,點![]() 在
在![]() 軸上的投影為
軸上的投影為![]() ,動點
,動點![]() 滿足
滿足![]() ,動點
,動點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)設![]() 的左頂點為
的左頂點為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 交于兩點
交于兩點![]() ,
,![]() (
(![]() ,
,![]() 不是左右頂點),且滿足
不是左右頂點),且滿足![]() ,求證:直線
,求證:直線![]() 恒過定點,并求出該定點的坐標.
恒過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() ,點
,點![]() 在橢圓
在橢圓![]() 上,橢圓
上,橢圓![]() 的離心率是
的離心率是![]() .
.
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)設點![]() 為橢圓長軸的左端點,
為橢圓長軸的左端點,![]() 為橢圓上異于橢圓
為橢圓上異于橢圓![]() 長軸端點的兩點,記直線
長軸端點的兩點,記直線![]() 斜率分別為
斜率分別為![]() ,若
,若![]() ,請判斷直線
,請判斷直線![]() 是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
是否過定點?若過定點,求該定點坐標,若不過定點,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年國際象棋奧林匹克團體賽中國男隊、女隊同時奪冠.國際象棋中騎士的移動規則是沿著3×2格或2×3格的對角移動.在歷史上,歐拉、泰勒、哈密爾頓等數學家研究了“騎士巡游”問題:在![]() 格的黑白相間的國際象棋棋盤上移動騎士,是否可以讓騎士從某方格內出發不重復地走遍棋盤上的每一格?
格的黑白相間的國際象棋棋盤上移動騎士,是否可以讓騎士從某方格內出發不重復地走遍棋盤上的每一格?
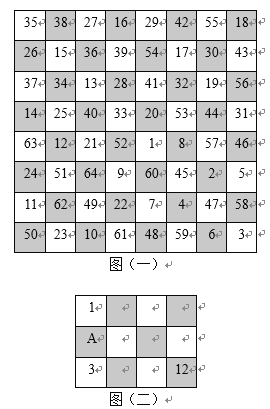
圖(一)給出了騎士的一種走法,它從圖上標1的方格內出發,依次經過標2,3,4,5,6,![]() ,到達標64的方格內,不重復地走遍棋盤上的每一格,又可從標64的方格內直接走回到標1的方格內.如果騎士的出發點在左下角標50的方格內,按照上述走法,_____(填“能”或“不能”)走回到標50的方格內.
,到達標64的方格內,不重復地走遍棋盤上的每一格,又可從標64的方格內直接走回到標1的方格內.如果騎士的出發點在左下角標50的方格內,按照上述走法,_____(填“能”或“不能”)走回到標50的方格內.
若騎士限制在圖(二)中的3×4=12格內按規則移動,存在唯一一種給方格標數字的方式,使得騎士從左上角標1的方格內出發,依次不重復經過2,3,4,5,6,![]() ,到達右下角標12的方格內,分析圖(二)中A處所標的數應為____.
,到達右下角標12的方格內,分析圖(二)中A處所標的數應為____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某超市在節日期間進行有獎促銷,凡在該超市購物滿![]() 元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有
元的顧客,將獲得一次摸獎機會,規則如下:一個袋子裝有![]() 只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵
只形狀和大小均相同的玻璃球,其中兩只是紅色,三只是綠色,顧客從袋子中一次摸出兩只球,若兩只球都是紅色,則獎勵![]() 元;共兩只球都是綠色,則獎勵
元;共兩只球都是綠色,則獎勵![]() 元;若兩只球顏色不同,則不獎勵.
元;若兩只球顏色不同,則不獎勵.
(1)求一名顧客在一次摸獎活動中獲得![]() 元的概率;
元的概率;
(2)記![]() 為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量
為兩名顧客參與該摸獎活動獲得的獎勵總數額,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com