【題目】選修4-4：坐標系與參數方程
在平面直角坐標系中，以坐標原點為極點， 
軸正半軸為極軸，建立極坐標系，點
的極坐標為
，直線
的極坐標方程為
，且
過點
，曲線
的參考方程為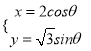
（
為參數）.
（1）求曲線
上的點到直線
的距離的最大值與最小值；
（2）過點
與直線
平行的直線
與曲
線交于
兩點，求
的值.
【答案】（1）
（2）
.
【解析】試題分析：（1）點A的極坐標為（4
， 
），可化為直角坐標A（4，4）．直線l的極坐標方程為ρcos（θ﹣
）=a，把點A的坐標代入直線方程可得a，再利用點到直線的距離公式與三角函數的單調性值域及其絕對值的性質即可得出．（2）寫出直線的參數方程，曲線C1的參數方程為（θ為參數），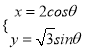
化為
，聯立解出，利用t的幾何意義得到
．
解析：
（1）由直線
過點
可得
，故
，
則易得直線
的直角坐標方程為
.
根據點到直線的距離方程可得曲線
上的點到直線
的距離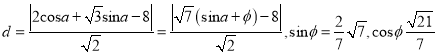
，
.
（2）由（1）知直線
的傾斜角為
，
則直線
的參數方程為
（
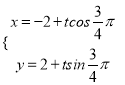為參數）.
又易知曲線
的普通方程為
.
把直線
的參數方程代入曲線
的普通方程可得
，
，依據參數
的幾何意義可知
.
小題狂做系列答案科目：高中數學 來源： 題型：
【題目】已知拋物線
上一點
到其焦點
的距離為4，橢圓
的離心率
，且過拋物線的焦點
.
（1）求拋物線
和橢圓
的標準方程；
（2）過點
的直線
交拋物線
于
兩不同點，交
軸于點
，已知
， 
，求證： 
為定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
各項均為正數， 
， 
，且
對任意
恒成立，記
的前
項和為
.
（1）若
，求
的值；
（2）證明：對任意正實數
， 
成等比數列；
（3）是否存在正實數
，使得數列
為等比數列.若存在，求出此時
和
的表達式；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
有極值，且在
處的切線與直線
垂直．
（1）求實數
的取值范圍；
（2）是否存在實數
，使得函數
的極小值為
．若存在，求出實數
的值；若不存在，請說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在直角坐標系
中，直線
的參數方程為
（
為參數），在以原點
為極點， 
軸正半軸為極軸的極坐標系中，圓
的方程為
．
（1）寫出直線
的普通方程和圓
的直角坐標方程；
（2）設點
，直線
與圓
相交于
兩點，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系中， 
為坐標原點， 
、
是雙曲線
上的兩個動點，動點
滿足
，直線
與直線
斜率之積為2，已知平面內存在兩定點
、
，使得
為定值，則該定值為________
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市一次全市高中男生身高統計調查數據顯示：全市
名男生的身高服從正態分布
．現從某學校高三年級男生中隨機抽取
名測量身高，測量發現被測學生身高全部介于
和
之間，將測量結果按如下方式分組： 
， 
，…， 
，得到的頻率分布直方圖如圖所示．
（Ⅰ）試評估該校高三年級男生在全市高中男生中的平均身高狀況；
（Ⅱ）求這
名男生身高在
以上（含
）的人數；
（Ⅲ）在這
名男生身高在
以上（含
）的人中任意抽取
人，該
人中身高排名（從高到低）在全市前
名的人數記力
，求
的數學期望．
參考數據：若
，則
，
， 
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
