
【題目】已知函數![]() ,
, ![]() ,函數
,函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸.
軸.
(1)求![]() 的值;
的值;
(2)求函數![]() 的極小值;
的極小值;
(3)設斜率為![]() 的直線與函數
的直線與函數![]() 的圖象交于兩點
的圖象交于兩點![]() ,
, ![]() ,
, ![]() ,證明:
,證明: ![]() .
.
【答案】(1) ![]() (2) 函數
(2) 函數![]() 的極小值為
的極小值為![]() .(3) 見解析
.(3) 見解析
【解析】試題分析:(1)由導數幾何意義得![]() ,解得
,解得![]() .(2)先求導函數零點,列表分析導函數符號變化規律,進而確定極小值點(3)先利用斜率公式化簡所證不等式
.(2)先求導函數零點,列表分析導函數符號變化規律,進而確定極小值點(3)先利用斜率公式化簡所證不等式![]() ,再利用換元
,再利用換元![]() 轉化為
轉化為![]() ,最后根據導數分別證明
,最后根據導數分別證明![]() 及
及![]()
試題解析:解:(1)依題意得![]() ,則
,則![]() .
.
由函數![]() 的圖象在點
的圖象在點![]() 處的切線平行于
處的切線平行于![]() 軸得:
軸得:
![]() ,所以
,所以![]() .
.
(2)由(1)得![]() ,
,
因為函數![]() 的定義域為
的定義域為![]() ,令
,令![]() 得
得![]() 或
或![]() .
.
函數![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;在
上單調遞減;在![]() 上單調遞增,
上單調遞增,
故函數![]() 的極小值為
的極小值為![]() .
.
(3)證法一:依題意得![]() ,
,
要證![]() ,即證
,即證![]() ,
,
因![]() ,即證
,即證![]() ,
,
令![]() ,即證
,即證![]() ,
,
令![]() ,則
,則![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,即
,即![]() ,所以
,所以![]() ①
①
令![]() ,則
,則![]() ,
,
所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,即
,即![]() ②
②
綜①②得![]() ,即
,即![]() .
.
證法二:依題意得![]() ,
,
令![]() ,則
,則![]() ,
,
由![]() 得
得![]() ,當
,當![]() 時,
時, ![]() ,當
,當![]() 時,
時, ![]() ,
,
所以![]() 在
在![]() 單調遞增,在
單調遞增,在![]() 單調遞減,又
單調遞減,又![]() ,
,
所以![]() ,即
,即![]() .
.


科目:高中數學 來源: 題型:
【題目】為豐富人民群眾業余生活,某市擬建設一座江濱公園,通過專家評審篩選處建設方案A和B向社會公開征集意見,有關部分用簡單隨機抽樣方法調查了500名市民對這兩種方案的看法,結果用條形圖表示如下:
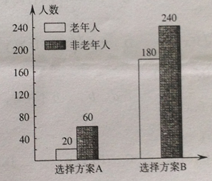
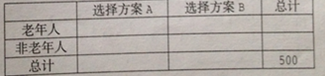
(1)根據已知條件完成下面![]() 列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過
列聯表,并用獨立性檢驗的方法分析,能否在犯錯誤的概率不超過![]() 的前提下認為是否選擇方案A和年齡段有關?
的前提下認為是否選擇方案A和年齡段有關?
(2)根據(1)的結論,能否提出一個更高的調查方法,使得調查結果更具代表性,說明理由.
附:

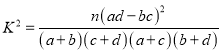
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】太極圖是由黑白兩個魚形紋組成的圖案,俗稱陰陽魚,太極圖展現了一種相互轉化,相互統一的和諧美.定義:能夠將圓![]() 的周長和面積同時等分成兩部分的函數稱為圓
的周長和面積同時等分成兩部分的函數稱為圓![]() 的一個“太極函數”.下列有關說法中:
的一個“太極函數”.下列有關說法中:

①對圓![]() 的所有非常數函數的太極函數中,一定不能為偶函數;
的所有非常數函數的太極函數中,一定不能為偶函數;
②函數![]() 是圓
是圓![]() 的一個太極函數;
的一個太極函數;
③存在圓![]() ,使得
,使得![]() 是圓
是圓![]() 的太極函數;
的太極函數;
④直線![]() 所對應的函數一定是圓
所對應的函數一定是圓![]() 的太極函數.
的太極函數.
所有正確說法的序號是__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數 ![]()
(1)當a<0時,判斷f(x)在(0,+∞)上的單調性;
(2)當a=﹣4時,對任意的實數x1 , x2∈[1,2],都有f(x1)≤g(x2),求實數m的取值范圍;
(3)當 ![]() ,
, 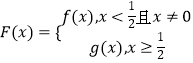 ,y=|F(x)|在(0,1)上單調遞減,求a的取值范圍.
,y=|F(x)|在(0,1)上單調遞減,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() )將
)將![]() 的圖象向右平移兩個單位,得到函數
的圖象向右平移兩個單位,得到函數![]() 的圖象.
的圖象.
(1)求函數![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且僅有一個實根,求
上有且僅有一個實根,求![]() 的取值范圍;
的取值范圍;
(3)若函數![]() 與
與![]() 的圖像關于直線
的圖像關于直線![]() 對稱,設
對稱,設![]() ,已知
,已知![]() 對任意的
對任意的![]() 恒成立,求
恒成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com