
| A. | 1 | B. | 2 | C. | $2\sqrt{2}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
分析 由條件利用函數的奇偶性、單調性可得 (x-3)2+(y-2)2≤1,表示以(3,2)為圓心、半徑等于1的圓及其內部區域.而 $\frac{y-2}{x}$的表示圓內的點(x,y)與點(0,2)連線的斜率,求出該圓的切線斜率,可得結論.
解答 解:∵對任意x,都有f(-x)+f(x)=0恒成立,即f(-x)=-f(x)恒成立,故函數f(x)為奇函數.
根據f(x)是定義在R上的增函數,f(x2-6x)+f(y2-4y+12)≤0,
可得 f(x2-6x)≤-f(y2-4y+12)=f(-y2+4y-12),即 x2-6x≤-y2+4y-12,
即x2-6x+y2-4y+12≤0,即 (x-3)2+(y-2)2≤1,表示以(3,2)為圓心、半徑等于1的圓及其內部區域.
而 $\frac{y-2}{x}$的表示圓內的點(x,y)與點(0,2)連線的斜率,
設過點(0,2)的圓的切線的斜率為k,則切線方程為y-2=k(x-0),即kx-y+2=0,
根據圓心(3,2)到切線的距離等于半徑,可得$\frac{|3k-2+2|}{\sqrt{{k}^{2}+1}}$=1,求得k=±$\frac{\sqrt{2}}{4}$,
可得$\frac{y-2}{x}$的最大值為$\frac{\sqrt{2}}{4}$,
故選:D.
點評 本題主要考查函數的奇偶性、單調性的應用,直線的斜率公式,直線和圓的位置關系,點到直線的距離公式,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
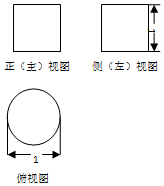
| A. | 2π | B. | π | C. | $\frac{π}{2}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
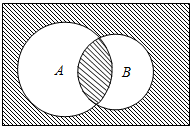
| A. | ∁UA∪(A∩B) | B. | ∁UA∩∁UB | C. | ∁UA∪∁UB | D. | ∁U(A∪B)∪(A∩B) |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com