
已知冪函數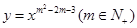 的圖象與x軸,y軸無交點且關于原點對稱,又有函數f(x)=x2-alnx+m-2在(1,2]上是增函數,g(x)=x-
的圖象與x軸,y軸無交點且關于原點對稱,又有函數f(x)=x2-alnx+m-2在(1,2]上是增函數,g(x)=x- 在(0,1)上為減函數.
在(0,1)上為減函數.
①求a的值;
②若 ,數列{an}滿足a1=1,an+1=p(an),(n∈N+),數列{bn},滿足
,數列{an}滿足a1=1,an+1=p(an),(n∈N+),數列{bn},滿足 ,
,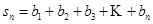 ,求數列{an}的通項公式an和sn.
,求數列{an}的通項公式an和sn.
③設 ,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
,試比較[h(x)]n+2與h(xn)+2n的大小(n∈N+),并說明理由.
①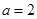 ;②
;②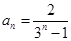 ;
;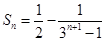 ;③見解析.
;③見解析.
【解析】
試題分析:①由冪函數的定義和性質可以知道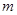 的取值集合,由圖像關于原點對稱的函數是奇函數可以確定
的取值集合,由圖像關于原點對稱的函數是奇函數可以確定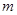 的值,將
的值,將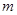 的值代入
的值代入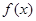 ,
,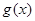 的解析式后,根據函數的單調性與導函數的關系以及不等式的恒成立問題的解法就可以知道
的解析式后,根據函數的單調性與導函數的關系以及不等式的恒成立問題的解法就可以知道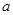 滿足的不等式,就可以解得
滿足的不等式,就可以解得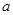 的值;②先由已知條件求出
的值;②先由已知條件求出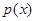 的解析式,然后得出
的解析式,然后得出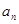 ,
,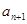 的關系,由函數構造的方法可以求得
的關系,由函數構造的方法可以求得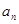 的解析式,代入
的解析式,代入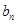 即可,再由數列求和公式求得
即可,再由數列求和公式求得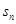 的值;③先求出
的值;③先求出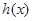 的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
的解析式,再由相減的方法來判斷兩個式子的大小,最后減得的結果和0比較即可,注意分類討論的思想.
試題解析:①冪函數的圖像與 軸,
軸, 軸無交點,則有
軸無交點,則有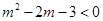 ,解得
,解得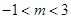
又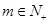 ,∴
,∴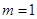 或
或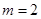 ,
,
又冪函數的圖像關于原點對稱,則有冪函數是奇函數,
當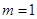 時,
時,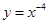 是偶函數,不合題意,舍去,
是偶函數,不合題意,舍去,
當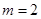 時,
時,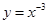 是奇函數,∴
是奇函數,∴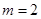 ,
,
∴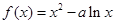 ,求導得
,求導得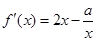 ,
,
又∵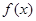 在
在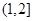 上是增函數,∴
上是增函數,∴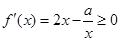 在
在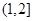 上恒成立,
上恒成立,
解得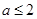 ,
,
又∵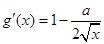 ,
,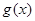 在
在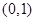 上為減函數,
上為減函數,
∴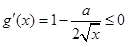 在
在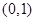 上恒成立,
上恒成立,
解得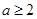 ,
,
綜上知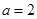 ;
..3分
;
..3分
②∵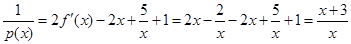 ,
,
∴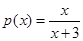 ∴
∴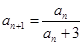 ∴
∴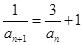 ∴
∴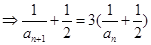 ,
,
∴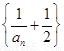 是首項為
是首項為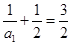 公比
公比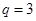 的等比數列,
的等比數列,
∴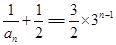 解得
解得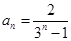 ,
,
∴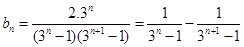 ,
,
∴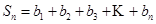 ,
,
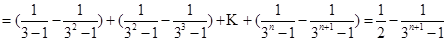 ;
.6分
;
.6分
③∵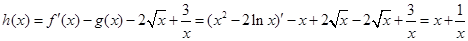 ,
,
當 時,
時,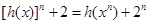 ,
,
當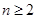 時,
時,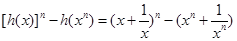
=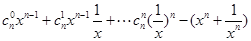
=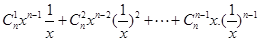
=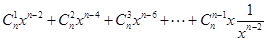
=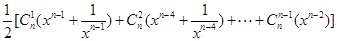
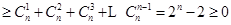 ,
,
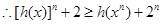 .
10分
.
10分
考點:函數的單調性與導函數的關系,奇函數圖像的性質,等比數列的構造.


科目:高中數學 來源:2010-2011學年廣東省茂名市高州市長坡中學高三(上)第二次月考數學試卷(解析版) 題型:選擇題
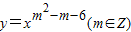 的圖象與x軸無公共點,則m的值的取值范圍是( )
的圖象與x軸無公共點,則m的值的取值范圍是( )查看答案和解析>>
科目:高中數學 來源:2011年福建省高考60天沖刺訓練數學試卷07(理科)(解析版) 題型:解答題
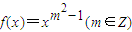 的圖象與x軸,y軸都無交點,且關于原點對稱,則函數f(x)的解析式是 .
的圖象與x軸,y軸都無交點,且關于原點對稱,則函數f(x)的解析式是 .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com