已知直線
、
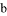和平面
、
，下列命題中假命題的是____________（只填序號）．
①若
，則平行于經過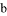的任何平面；
②若
，
，則；
③若，
，且
，則
；
④若
，且，則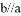
．
科目：高中數學 來源：2016-2017學年山東省膠州市高二上學期期末考試文數試卷（解析版） 題型：解答題
如圖,在四棱錐
中,底面
為平行四邊形, 
為側棱
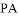的中點.
（Ⅰ）求證: 
∥平面
（Ⅱ）若
,
,
求證:平面
平面
查看答案和解析>>
科目：高中數學 來源：2017屆陜西省西安市高三模擬（一）數學（理）試卷（解析版） 題型：解答題
某研究小組在電腦上進行人工降雨模擬實驗，準備用
、
、
三種人工降雨方式分別對甲、乙、丙三地實施人工降雨，其試驗數據統計如表：
方式 | 實施地點 | 大雨 | 中雨 | 小雨 | 模擬實驗總次數 |
| 甲 | 4次 | 6次 | 2次 | 12次 |
| 乙 | 3次 | 6次 | 3次 | 12次 |
| 丙 | 2次 | 2次 | 8次 | 12次 |
假定對甲、乙、丙三地實施的人工降雨彼此互不影響，請你根據人工降雨模擬實驗的統計數據：
（Ⅰ）求甲、乙、丙三地都恰為中雨的概率；
（Ⅱ）考慮到旱情和水土流失，如果甲地恰需中雨即達到理想狀態，乙地必須是大雨才達到理想狀態，丙地只能是小雨或中雨即達到理想狀態，記“甲、乙、丙三地中達到理想狀態的個數”為隨機變量
，求隨機變量的分布列和數學期望
．
查看答案和解析>>
科目：高中數學 來源：2017屆陜西省西安市高三模擬（一）數學（理）試卷（解析版） 題型：選擇題
公元263年左右，我國數學家劉徽發現，當圓內接多邊形的邊數無限增加時，多邊形面積可無限逼近圓的面積，由此創立了割圓術，利用割圓術劉徽得到了圓周率精確到小數點后面兩位的近似值3.14，這就是著名的徽率．如圖是利用劉徽的割圓術設計的程序框圖，則輸出的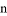
值為（ ）
參考數據：
，
，
．
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目：高中數學 來源：2017屆陜西省西安市高三模擬（一）數學（理）試卷（解析版） 題型：選擇題
在復平面內，兩個共軛復數所對應的點（ ）
A. 關于
軸對稱 B. 關于
軸對稱 C. 關于原點對稱 D. 關于直線
對稱
查看答案和解析>>
科目：高中數學 來源：2017屆遼寧省沈陽市郊聯體高三上學期期末考試文數試卷（解析版） 題型：選擇題
如圖，有一個水平放置的透明無蓋的正方體容器，容器高8
，將一個球放在容器口，再向容器注水，當球面恰好接觸水面時測得水深為6，如不計容器的厚度，則球的表面積為（ ）
A. 
B. 
C. 
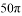D. 
查看答案和解析>>
科目：高中數學 來源：2017屆山東省膠州市高三上學期期末考試數學（理）試卷（解析版） 題型：選擇題
定義：如果函數
在
上存在
，滿足
，
，則稱函數在上的“雙中值函數”，已知函數
是
上“雙中值函數”，則實數
的取值范圍是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
在
上為增函數，則
的取值范圍是__________．
與圓
的位置關系是( )