
已知函數
(1)若不等式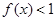 的解集為
的解集為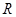 ,求
,求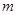 的取值范圍;
的取值范圍;
(2)解關于 的不等式
的不等式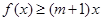 ;
;
(3)若不等式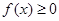 對一切
對一切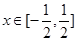 恒成立,求
恒成立,求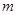 的取值范圍.
的取值范圍.
(1)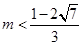 ,(2)①當
,(2)①當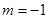 時,解集為
時,解集為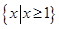 ;②當
;②當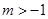 時,解集為
時,解集為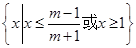 ;③當
;③當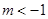 時,解集為R;(3)
時,解集為R;(3)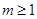
【解析】
試題分析:(1)①當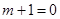 即
即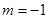 時,
時,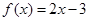 ,不合題意; 1分
,不合題意; 1分
②當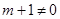 即
即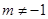 時,
時,
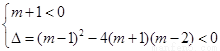 ,即
,即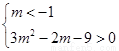 ,
3分
,
3分
∴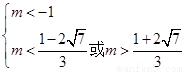 ,∴
,∴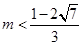 5分
5分
(2)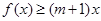 即
即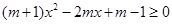
即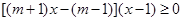
①當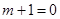 即
即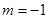 時,解集為
時,解集為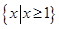 7分
7分
②當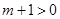 即
即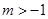 時,
時,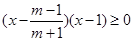
∵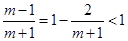 ,∴解集為
,∴解集為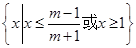 9分
9分
③當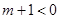 即
即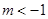 時,
時,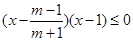
∵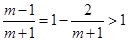 ,∴解集為R 11分
,∴解集為R 11分
(3)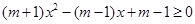 ,即
,即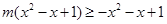 ,
,
∵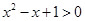 恒成立,∴
恒成立,∴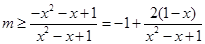 13分
13分
設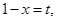 則
則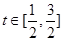 ,
,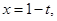
∴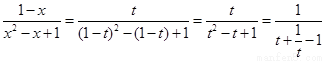 ,
,
∵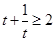 ,當且僅當
,當且僅當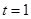 時取等號,∴
時取等號,∴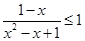 ,當且僅當
,當且僅當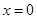 時取等號,
時取等號,
∴當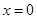 時,
時,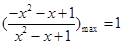 ,∴
,∴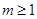 16分
16分
考點:本題考查了含參一元二次不等式的的解法及恒成立問題
點評:在解關于含參數的一元二次不等式時,往往都要對參數進行分類討論.為了要做到分類“不重不漏”,討論時需注意分類的標準.


 字詞句篇與同步作文達標系列答案
字詞句篇與同步作文達標系列答案科目:高中數學 來源:2012-2013學年陜西省西安市華清中學高三(下)自主命題數學試卷2(文科)(解析版) 題型:解答題
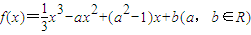
查看答案和解析>>
科目:高中數學 來源:2014屆江蘇省東臺市高二下學期期中考試理科數學試卷(解析版) 題型:解答題
已知函數
(1)若對任意的 恒成立,求實數
恒成立,求實數 的最小值.
的最小值.
(2)若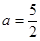 且關于
且關于 的方程
的方程 在
在 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數 的取值范圍;
的取值范圍;
(3)設各項為正的數列 滿足:
滿足: 求證:
求證:
查看答案和解析>>
科目:高中數學 來源:2013屆江蘇省無錫市高二下期中數學試卷(成志班)(解析版) 題型:解答題
已知函數
(1)若對任意的 恒成立,求實數
恒成立,求實數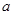 的最小值.
的最小值.
(2)若 且關于
且關于 的方程
的方程 在
在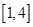 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數 的取值范圍;
的取值范圍;
(3)設各項為正的數列 滿足:
滿足: 求證:
求證:
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第一次月考試卷理科數學 題型:解答題
已知函數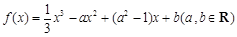
(1)若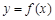 的圖象在點
的圖象在點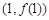 處的切線方程為
處的切線方程為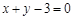 ,求
,求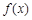 在區間
在區間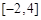 上的最大值;
上的最大值;
(2)當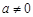 時,若
時,若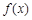 在區間
在區間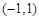 上不單調,求
上不單調,求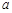 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2013屆福建省高一下學期期末模塊測試數學試題 題型:解答題
(本題滿分13分)
已知函數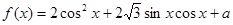 .
.
(1) 若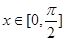 且
且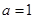 時,求
時,求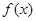 的最大值和最小值,以及取得最大值和最小值時
的最大值和最小值,以及取得最大值和最小值時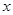 的
的
值;
(2) 若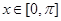 且
且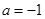 時,方程
時,方程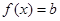 有兩個不相等的實數根
有兩個不相等的實數根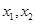 ,求
,求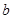 的取值
的取值
范圍及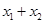 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com