
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
分析 利用已知條件求出雙曲線方程,然后通過其它體積求出雙曲線的標(biāo)準(zhǔn)方程,即可判斷選項.
解答 解:對于①,∵||PF1|-|PF2||=2a=6,∴a=3
又∵焦點為F1(-5,0),F(xiàn)2(5,0),∴c=5
∴離心率e=$\frac{5}{3}$,故①符合條件;
對于②,雙曲線C的虛軸長為4,∴b=2,a=$\sqrt{21}$
∴離心率e=$\frac{5}{\sqrt{21}}$,故②不符合條件;
對于③,雙曲線C的一個頂點與拋物線y2=6x的焦點重合,
∴a=$\frac{3}{2}$,e=$\frac{10}{3}$,故③不符合條件;
對于④,∵漸近線方程為3x+4y=0
∴$\frac{b}{a}$=$\frac{3}{4}$,
又∵c=5,c2=a2+b2,∴a=4
∴離心率e=$\frac{5}{4}$,故④不符合條件.
故選:A.
點評 本題考查雙曲線的簡單性質(zhì),標(biāo)準(zhǔn)方程的求法,命題的真假的判斷,是基礎(chǔ)題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
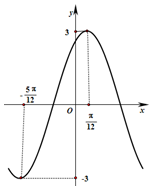 函數(shù)y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則此函數(shù)的解析式為y=3sin(2x+$\frac{π}{3}$).
函數(shù)y=Asin(ω•x+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分圖象如圖所示,則此函數(shù)的解析式為y=3sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | 向右平移$\frac{π}{6}$個單位長度 | B. | 向右平移$\frac{π}{12}$個單位長度 | ||
| C. | 向左平移$\frac{π}{6}$個長度單位 | D. | 向左平移$\frac{π}{12}$個長度單位 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:選擇題
| A. | -1-3i | B. | $\sqrt{5}$ | C. | 10 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com