
【題目】為緩解堵車現象,解決堵車問題,銀川市交警隊調查了甲乙兩個路口的車流量,在2019年6月隨機選取了14天,統計每天上午7:30-9:00早高峰時段各自的車流量(單位:百輛)得到如圖所示的莖葉圖,根據莖葉圖回答以下問題.

(1)甲乙兩個路口的車流量的中位數分別是多少?
(2)試計算甲乙兩個路口的車流量在![]() 之間的頻率.
之間的頻率.
科目:高中數學 來源: 題型:
【題目】袋中裝有紅球3個、白球2個、黑球1個,從中任取2個,則互斥而不對立的兩個事件是![]()
![]()
A. 至少有一個白球;都是白球 B. 至少有一個白球;至少有一個紅球
C. 至少有一個白球;紅、黑球各一個 D. 恰有一個白球;一個白球一個黑球
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 在
在![]() 上是減函數,在
上是減函數,在![]() 上是增函數
上是增函數![]() 若函數
若函數![]() ,利用上述性質,
,利用上述性質,
![]() Ⅰ
Ⅰ![]() 當
當![]() 時,求
時,求![]() 的單調遞增區間
的單調遞增區間![]() 只需判定單調區間,不需要證明
只需判定單調區間,不需要證明![]() ;
;
![]() Ⅱ
Ⅱ![]() 設
設![]() 在區間
在區間![]() 上最大值為
上最大值為![]() ,求
,求![]() 的解析式;
的解析式;
![]() Ⅲ
Ⅲ![]() 若方程
若方程![]() 恰有四解,求實數a的取值范圍.
恰有四解,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2016年11月3日20點43分我國長征運載火箭在海南文昌發射中心成功發射,它被公認為我國已從航天大國向航天強國邁進的重要標志.長征五號運載火箭的設計生產采用很多新材料,甲工廠承擔了某種材料的生產,并以![]() 千克/時的速度勻速生產(為保證質量要求
千克/時的速度勻速生產(為保證質量要求![]() ),每小時可消耗
),每小時可消耗![]() 材料
材料![]() 千克,已知每小時生產1千克該產品時,消耗
千克,已知每小時生產1千克該產品時,消耗![]() 材料10千克.
材料10千克.
(1)設生產![]() 千克該產品,消耗
千克該產品,消耗![]() 材料
材料![]() 千克,試把
千克,試把![]() 表示為
表示為![]() 的函數.
的函數.
(2)要使生產1000千克該產品消耗的![]() 材料最少,工廠應選取何種生產速度?并求消耗的
材料最少,工廠應選取何種生產速度?并求消耗的![]() 材料最少為多少?
材料最少為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,有一塊矩形空地,要在這塊空地上開辟一個內接四邊形為綠地,使其四個頂點分別落在矩形的四條邊上,已知![]() 且
且![]() 設
設![]() ,綠地面積為
,綠地面積為![]() .
.
(1)寫出![]() 關于
關于![]() 的函數關系式,并指出這個函數的定義域.
的函數關系式,并指出這個函數的定義域.
(2)當![]() 為何值時,綠地面積
為何值時,綠地面積![]() 最大?
最大?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,且
,且![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)設![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,求使不等式
,求使不等式![]() 對一切
對一切![]() 都成立的正整數
都成立的正整數![]() 的最大值.
的最大值.
(3)設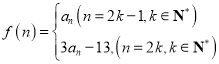 ,是否存在
,是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】首屆世界低碳經濟大會在南昌召開,本屆大會以“節能減排,綠色生態”為主題,某單位在國家科研部門的支持下,進行技術攻關,采用了新工藝,把二氧化碳轉化為一種可利用的化工產品.已知該單位每月的處理量最少為400噸,最多為600噸,月處理成本![]() (元)與月處理量
(元)與月處理量![]() (噸)之間的函數關系可近似地表示為
(噸)之間的函數關系可近似地表示為![]() ,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
,且每處理一噸二氧化碳得到可利用的化工產品價值為100元.
(1)該單位每月處理量為多少噸時,才能使每噸的平均處理成本最低?
(2)該單位每月能否獲利?如果獲利,求出最大利潤;如果不獲利,則需要國家至少補貼多少元才能使該單位不虧損?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是邊長為
是邊長為![]() 的正方形,
的正方形,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是線段
是線段![]() 上異于端點的一點,平面
上異于端點的一點,平面![]()
![]() 平面
平面![]() ,
,![]() .
.

(Ⅰ)證明:![]() ;
;
(Ⅱ)若![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】巳知集合P={![]() },Q={
},Q={![]() },將P∪Q的所有元素從小到大依次排列構成一個數列{
},將P∪Q的所有元素從小到大依次排列構成一個數列{![]() },記
},記![]() 為數列{
為數列{![]() }的前n項和,則使得
}的前n項和,則使得![]() <1000成立的
<1000成立的![]() 的最大值為
的最大值為
A. 9 B. 32 C. 35 D. 61
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com