Question

【題目】已知數(shù)列的前項和為，且.

（1）求數(shù)列的通項公式；

（2）設(shè)，數(shù)列的前項和為，求使不等式對一切都成立的正整數(shù)的最大值.

（3）設(shè)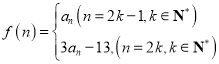，是否存在，使得成立?若存在，求出的值；若不存在，請說明理由.

Answer 1

【答案】（1）（2）672（3）不存在，理由見解析

【解析】

（1）由數(shù)列的遞推式，計算可得所求通項公式；

（2）求得，運用裂項相消求和可得，判斷的單調(diào)性，可得最小值，即可得到的最大值；

（3）討論為奇數(shù)或偶數(shù)，假設(shè)存在，計算可判斷是否存在．

解：（1）因為，所以，又因為滿足上式，所以.

（2）由（1）可知，所以，顯然隨著的增大而增大，故的最小值為，由可得.

（3）結(jié)論：不存在滿足條件的.

理由如下:①當(dāng)為奇數(shù)時為偶數(shù)，則，即，所以，解得，矛盾.

②當(dāng)為偶數(shù)時為奇數(shù)，則，即，所以，解得，矛盾.綜上所述，不存在滿足條件的.