
| A. | 2 | B. | $2\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | 4 |
分析 由二倍角的余弦公式和基本不等式,化簡整理,計算即可得到所求最小值.
解答 解:$\frac{{1+cos2x+4{{sin}^2}x}}{sin2x}$=$\frac{2co{s}^{2}x+4si{n}^{2}x}{2sinxcosx}$=$\frac{cosx}{sinx}$+$\frac{2sinx}{cosx}$,
由x為第三象限角,可得sinx<0,cosx<0,
由基本不等式可得,$\frac{cosx}{sinx}$+$\frac{2sinx}{cosx}$≥2$\sqrt{\frac{cosx}{sinx}•\frac{2sinx}{cosx}}$=2$\sqrt{2}$,
當且僅當$\frac{cosx}{sinx}$=$\frac{2sinx}{cosx}$時,取得最小值2$\sqrt{2}$.
故選:B.
點評 本題考查三角函數的最值的求法,注意運用二倍角公式和基本不等式化簡整理,考查運算能力,屬于中檔題.


科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{101}{99}$ | B. | 3 | C. | $\frac{99}{101}$ | D. | $\frac{99}{100}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (-$\frac{8}{9}$,8] | B. | [-$\frac{8}{9}$,8] | C. | ($\frac{1}{9}$,9) | D. | [$\frac{1}{9}$,9] |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 33 | B. | -3 | C. | 7 | D. | -7 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
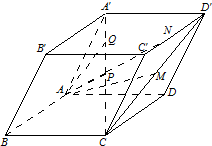 如圖,在平行六面體ABCD-A′B′C′D′中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AA'}=\overrightarrow c$,P是CA′的中點,M是CD′的中點,N是C′D′的中點,點Q在CA′上,且CQ:QA′=4:1,試用基向量$\{\overrightarrow a,\overrightarrow{b},\overrightarrow c\}$表示以下向量:
如圖,在平行六面體ABCD-A′B′C′D′中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,\overrightarrow{AA'}=\overrightarrow c$,P是CA′的中點,M是CD′的中點,N是C′D′的中點,點Q在CA′上,且CQ:QA′=4:1,試用基向量$\{\overrightarrow a,\overrightarrow{b},\overrightarrow c\}$表示以下向量:查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com