
分析 (1)當n=5時,$(1-\frac{x}{2})^{10}$=${a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}$+…+${a}_{10}{x}^{10}$,ai=${∁}_{10}^{i}$$(-\frac{1}{2})^{i}$,假設|ak|最大.則$\left\{\begin{array}{l}{{∁}_{10}^{k}(\frac{1}{2})^{k}≥{∁}_{10}^{k+1}(\frac{1}{2})^{k+1}}\\{{∁}_{10}^{k}(\frac{1}{2})^{k}≥{∁}_{10}^{k-1}(\frac{1}{2})^{k-1}}\end{array}\right.$,解得k即可得出.
(2)a3=-$\frac{1}{2}$,則${∁}_{2n}^{3}$$(-\frac{1}{2})^{3}$=-$\frac{1}{2}$,化為:2n3-3n2+n-6=0,解得n.
(3)an=${∁}_{2n}^{n}$$(-\frac{1}{2})^{n}$≤${∁}_{2n}^{n}$$(\frac{1}{2})^{n}$,要證明an<$\frac{2^n}{{\sqrt{2n+1}}}$(n∈N*).只要證明:${∁}_{2n}^{n}$$(\frac{1}{2})^{n}$<$\frac{2^n}{{\sqrt{2n+1}}}$(n∈N*).即要證明:${∁}_{2n}^{n}$<$\frac{{4}^{n}}{\sqrt{2n+1}}$.利用數學歸納法證明即可得出.
解答 (1)解:當n=5時,$(1-\frac{x}{2})^{10}$=${a}_{0}+{a}_{1}x+{a}_{2}{x}^{2}$+…+${a}_{10}{x}^{10}$,ai=${∁}_{10}^{i}$$(-\frac{1}{2})^{i}$,假設|ak|最大.則$\left\{\begin{array}{l}{{∁}_{10}^{k}(\frac{1}{2})^{k}≥{∁}_{10}^{k+1}(\frac{1}{2})^{k+1}}\\{{∁}_{10}^{k}(\frac{1}{2})^{k}≥{∁}_{10}^{k-1}(\frac{1}{2})^{k-1}}\end{array}\right.$,解得$\frac{8}{3}≤k≤\frac{11}{3}$,解得k=3.∴當k=3時,a3=${∁}_{10}^{3}(-\frac{1}{2})^{3}$=-15最小.
a2=${∁}_{10}^{2}(-\frac{1}{2})^{2}$=$\frac{45}{4}$,a4=${∁}_{10}^{4}$$(-\frac{1}{2})^{4}$=$\frac{105}{8}$>a2,∴a4最大.
(2)解:a3=-$\frac{1}{2}$,則${∁}_{2n}^{3}$$(-\frac{1}{2})^{3}$=-$\frac{1}{2}$,化為:2n3-3n2+n-6=0,∴(n-2)(2n2+n+3)=0,解得n=2.
(3)證明:∵an=${∁}_{2n}^{n}$$(-\frac{1}{2})^{n}$≤${∁}_{2n}^{n}$$(\frac{1}{2})^{n}$,要證明an<$\frac{2^n}{{\sqrt{2n+1}}}$(n∈N*).只要證明:${∁}_{2n}^{n}$$(\frac{1}{2})^{n}$<$\frac{2^n}{{\sqrt{2n+1}}}$(n∈N*).即要證明:${∁}_{2n}^{n}$<$\frac{{4}^{n}}{\sqrt{2n+1}}$.下面利用數學歸納法證明:(i)當n=1時,${∁}_{2}^{1}$=2<$\frac{4}{\sqrt{3}}$,因此成立.
(ii)假設當n=k∈N*時,${∁}_{2k}^{k}$<$\frac{{4}^{k}}{\sqrt{2k+1}}$.則n=k+1時,${∁}_{2k+2}^{k+1}$=$\frac{(2k+2)!}{(k+1)!(k+1)!}$=$\frac{(2k+2)(2k+1)(2k)!}{(k+1)^{2}k!k!}$<$\frac{2(2k+1)}{(k+1)}$•$\frac{{4}^{k}}{\sqrt{2k+1}}$=$\frac{\sqrt{2k+1}•{4}^{k+1}}{\sqrt{4{k}^{2}+8k+4}}$<$\frac{\sqrt{2k+1}•{4}^{k+1}}{\sqrt{4{k}^{2}+8k+3}}$<$\frac{{4}^{k+1}}{\sqrt{2k+3}}$,因此n=k+1時也成立.
綜上可得:an<$\frac{2^n}{{\sqrt{2n+1}}}$(n∈N*)成立.
點評 本題考查了二項式定理的應用、組合數的計算公式、數學歸納法、不等式的性質、放縮法,考查了推理能力與計算能力,屬于中檔題.


 暑假作業暑假快樂練西安出版社系列答案
暑假作業暑假快樂練西安出版社系列答案科目:高中數學 來源: 題型:選擇題
| A. | (x+2)2+(y-2)2=4 | B. | (x-2)2+(y+2)2=4 | C. | (x+2)2+(y+2)2=4 | D. | (x-2)2+(y-2)2=4 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
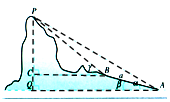 如圖,在山腳A測得山頂P的仰角為60°,沿傾斜角為15°的斜坡向上走200米到B,在B處測得山頂P的仰角為75°,則山高h=150($\sqrt{6}$+$\sqrt{2}$)米.
如圖,在山腳A測得山頂P的仰角為60°,沿傾斜角為15°的斜坡向上走200米到B,在B處測得山頂P的仰角為75°,則山高h=150($\sqrt{6}$+$\sqrt{2}$)米.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | f(0)+f(2)<2f(1) | B. | f(0)+f(2)=2f(1) | C. | f(0)<f(1)<f(2) | D. | f(0)+f(2)>2f(1) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | (2,3) | B. | (3,4) | C. | (1,3) | D. | (2,4) |
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com