
霧霾大氣嚴重影響人們生活,某科技公司擬投資開發新型節能環保產品,策劃部制定投資計劃時,不僅要考慮可能獲得的盈利,而且還要考慮可能出現的虧損,經過市場調查,公司打算投資甲、乙兩個項目,根據預測,甲、乙項目可能的最大盈利率分別為100%和60%,可能的最大虧損率分別為20%和10%,投資人計劃投資金額不超過10萬元要求確保可能的資金虧損不超過1.6萬元.
(1)若投資人用 萬元投資甲項目,
萬元投資甲項目, 萬元投資乙項目,試寫出
萬元投資乙項目,試寫出 、
、 所滿足的條件,并在直角坐標系內做出表示
所滿足的條件,并在直角坐標系內做出表示 、
、 范圍的圖形;
范圍的圖形;
(2)根據(1)的規劃,投資公司對甲、乙兩個項目投資多少萬元,才能是可能的盈利最大?
(1)如圖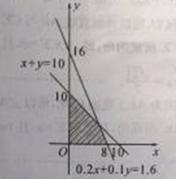 ;
;
(2)用6萬元投資甲項目,4萬元投資乙項目.
解析試題分析:(1)根據已知條件列出不等式組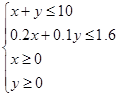 ,再在平面直角坐標系中畫出對應的可行域,注意邊界上的點也滿足條件;(2)主要是利用可行域求解線性目標函數的最大值即得投資公司獲得的最大利潤,圖解法解決含有實際背景的線性規劃問題的基本步驟是:①列出約束條件,確定目標函數;②畫出不等式(組)表示的平面區域;③作平行直線系使之與可行域有交點,求得最優解;④寫出目標函數的最值,并下結論.
,再在平面直角坐標系中畫出對應的可行域,注意邊界上的點也滿足條件;(2)主要是利用可行域求解線性目標函數的最大值即得投資公司獲得的最大利潤,圖解法解決含有實際背景的線性規劃問題的基本步驟是:①列出約束條件,確定目標函數;②畫出不等式(組)表示的平面區域;③作平行直線系使之與可行域有交點,求得最優解;④寫出目標函數的最值,并下結論.
試題解析:(1)由題意,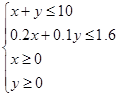 上述不等式組表示的平面區域如圖中陰影部分(含邊界),
上述不等式組表示的平面區域如圖中陰影部分(含邊界),
根據(1)的規劃和題設條件,可知目標函數為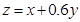 ,作直線
,作直線 ,并作平行于直線
,并作平行于直線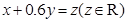 與可行域相交,當平行直線經過直線
與可行域相交,當平行直線經過直線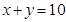 與
與 的交點
的交點 時,其截距最大,解方程組
時,其截距最大,解方程組 ,解得
,解得 ,即
,即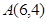 ,
,
此時 (萬元),
(萬元),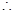 當
當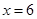 ,
,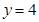 時,
時, 取得最大值.
取得最大值.
即投資人用6萬元投資甲項目,4萬元投資乙項目,才能確保虧損不超過1.6萬元,使可能的利潤最大.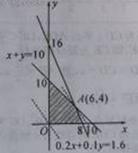
考點:用線性規劃解決實際問題,投資利潤最大問題.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:高中數學 來源: 題型:解答題
一農民有基本農田2畝,根據往年經驗,若種水稻,則每季畝產量為400公斤;若種花生,則每季畝產量為100公斤.但水稻成本較高,每季每畝240元,而花生只需80元;且花生每公斤賣5元,稻米每公斤賣3元.現該農民手頭有400元,兩種作物各種多少,才能獲得最大收益?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某公司計劃2014年在A,B兩個電視臺做總時間不超過300分鐘的廣告,廣告總費用不超過9萬元.A,B兩個電視臺的廣告收費標準分別為500元/分鐘和200元/分鐘,假定A,B兩個電視臺為該公司所做的每分鐘廣告,能給公司帶來的收益分別為0.3萬元和0.2萬元.問該公司如何分配在兩個電視臺做廣告的時間,才能使公司的收益最大?最大收益是多少萬元?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某營養師要為某個兒童預訂午餐和晚餐.已知一個單位的午餐含12個單位的碳水化合物、6個單位的蛋白質和6個單位的維生素C;一個單位的晚餐含8個單位的碳水化合物、6個單位的蛋白質和10個單位的維生素C.另外,該兒童這兩餐需要的營養中至少含64個單位的碳水化合物、42個單位的蛋白質和54個單位的維生素C.
如果一個單位的午餐、晚餐的費用分別是2.5元和4元,那么要滿足上述的營養要求,并且花費最少,應當為該兒童分別預訂多少個單位的午餐和晚餐?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某廠生產甲、乙兩種產品每噸所需的煤、電和產值如下表所示.
但國家每天分配給該廠的煤、電有限, 每天供煤至多56噸,供電至多450千瓦,問該廠如何安排生產,使得該廠日產值最大?最大日產值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
在一個居民小區內設計一個邊長為5米的菱形噴水池,規劃要求菱形的一條對角線長
不大于6米,另一條長 不小于6米,則菱形噴水池的兩條對角線的長度之和
不小于6米,則菱形噴水池的兩條對角線的長度之和 的
的
最大值為 米.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com