
【題目】已知函數f(x)=x+![]() +2(m為實常數).
+2(m為實常數).
(1)若函數f(x)圖象上動點P到定點Q(0,2)的距離的最小值為![]() ,求實數m的值;
,求實數m的值;
(2)若函數y=f(x)在區間[2,+∞)上是增函數,試用函數單調性的定義求實數m的取值范圍;
(3)設m<0,若不等式f(x)≤kx在x∈[![]() ,1]時有解,求k的取值范圍.
,1]時有解,求k的取值范圍.
【答案】(1) ![]() 或
或![]() ;(2)(-∞,4];(3)答案見解析.
;(2)(-∞,4];(3)答案見解析.
【解析】試題分析:
(1)設P(x,y),結合兩點之間距離公式有: ![]() ,求解關于實數
,求解關于實數![]() 的方程可得
的方程可得![]() 或
或![]() ;
;
(2)由題意知,任取x1,x2∈[2,+∞),且x1<x2,有f(x2)-f(x1)=(x2-x1)·![]() >0.則m<x1x2.據此可得m的取值范圍是(-∞,4].
>0.則m<x1x2.據此可得m的取值范圍是(-∞,4].
(3)由f(x)≤kx分離參數可得: ![]() 在
在![]() 上能成立,換元令
上能成立,換元令![]() ,結合二次函數的性質可得:
,結合二次函數的性質可得:
當![]() 時,k∈[4m+5,+∞);
時,k∈[4m+5,+∞);
當![]() 時,k∈[m+3,+∞).
時,k∈[m+3,+∞).
試題解析:
(1)設P(x,y),則y=x+![]() +2,
+2,
PQ2=x2+(y-2)2=x2+(x+![]() )2
)2
=2x2+![]() +2m≥2
+2m≥2![]() |m|+2m=2,
|m|+2m=2,
當m>0時,解得m=![]() -1;
-1;
當m<0時,解得m=-![]() -1.
-1.
所以m=![]() -1或m=-
-1或m=-![]() -1.
-1.
(2)由題意知,任取x1,x2∈[2,+∞),且x1<x2,
則f(x2)-f(x1)=x2+![]() +2-(x1+
+2-(x1+![]() +2)=(x2-x1)·
+2)=(x2-x1)·![]() >0.
>0.
因為x2-x1>0,x1x2>0,
所以x1x2-m>0,即m<x1x2.
由x2>x1≥2,得x1x2>4,所以m≤4.
所以m的取值范圍是(-∞,4].
(3)由f(x)≤kx,得x+![]() +2≤kx.
+2≤kx.
因為x∈[![]() ,1],所以k≥
,1],所以k≥![]() +
+![]() +1.
+1.
令t=![]() ,則t∈[1,2],
,則t∈[1,2],
所以k≥mt2+2t+1.
令g(t)=mt2+2t+1,t∈[1,2],
于是,要使原不等式在x∈[![]() ,1]時有解,當且僅當k≥[g(t)]min(t∈[1,2]).
,1]時有解,當且僅當k≥[g(t)]min(t∈[1,2]).
因為m<0,
所以g(t)=m(t+![]() )2+1-
)2+1-![]() 的圖象開口向下,
的圖象開口向下,
對稱軸為直線t=-![]() >0.
>0.
因為t∈[1,2],所以當0<-![]() ≤
≤![]() ,
,
即m≤-![]() 時,g(t)min=g(2)=4m+5;
時,g(t)min=g(2)=4m+5;
當-![]() >
>![]() ,即-
,即-![]() <m<0時,
<m<0時,
g(t)min=g(1)=m+3.
綜上,當m≤-![]() 時,k∈[4m+5,+∞);
時,k∈[4m+5,+∞);
當-![]() <m<0時,k∈[m+3,+∞).
<m<0時,k∈[m+3,+∞).


科目:高中數學 來源: 題型:
【題目】函數f(x)=a![]() -2ln x(a∈R).
-2ln x(a∈R).
(Ⅰ)當a=2時,求曲線f(x)在x=2處的切線方程;
(Ⅱ)若a>![]() ,且m,n分別為f(x)的極大值和極小值,S=m-n,求證:S<
,且m,n分別為f(x)的極大值和極小值,S=m-n,求證:S<![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856288)
設函數f(x)=aln x-x,g(x)=aex-x,其中a為正實數.
(Ⅰ)若f(x)在(1,+∞)上是單調減函數,且g(x)在(2,+∞)上有最小值,求a的取值范圍;
(Ⅱ)若函數f(x)與g(x)都沒有零點,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】共享單車是指企業的校園,地鐵站點、公交站點、居民區、商業區、公共服務區等提供自行車單車共享服務,是一種分時租賃模式,某共享單車企業為更好服務社會,隨機調查了100人,統計了這100人每日平均騎行共享單車的時間(單位:分鐘),由統計數據得到如下頻率分布直方圖,已知騎行時間在![]() 三組對應的人數依次成等差數列
三組對應的人數依次成等差數列
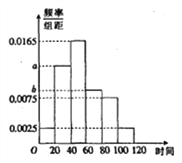
(1)求頻率分布直方圖中![]() 的值.
的值.
(2)若將日平均騎行時間不少于80分鐘的用戶定義為“忠實用戶”,將日平均騎行時間少于40分鐘的用戶為“潛力用戶”,現從上述“忠實用戶”與“潛力用戶”的人中按分層抽樣選出5人,再從這5人中任取3人,求恰好1人為“忠實用戶”的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-5:不等式選講]
已知函數f(x)=|2x+1|﹣|2x﹣3|,g(x)=|x+1|+|x﹣a|.
(l)求f(x)≥1的解集;
(2)若對任意的t∈R,s∈R,都有g(s)≥f(t).求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(導學號:05856295)德國大數學家高斯年少成名,被譽為數學王子.19歲的高斯得到了一個數學史上非常重要的結論,就是《正十七邊形尺規作圖之理論與方法》, 在其年幼時,對1+2+3+…+100的求和運算中,提出了倒序相加法的原理,該原理基于所給數據前后對應項的和呈現一定的規律生成,因此,此方法也被稱為高斯算法.現有函數f(x)=![]() ,則f(1)+f(2)+…+f(m+2017)等于( )
,則f(1)+f(2)+…+f(m+2017)等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,若f(x)≥2ln x在[1,+∞)上恒成立,則a的取值范圍是( )
,若f(x)≥2ln x在[1,+∞)上恒成立,則a的取值范圍是( )
A. (1,+∞) B. [1,+∞)
C. (2,+∞) D. [2,+∞)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com