
【題目】對于定義在![]() 上的函數
上的函數![]() ,若存在正常數
,若存在正常數![]() 、
、![]() ,使得
,使得![]() 對一切
對一切![]() 均成立,則稱
均成立,則稱![]() 是“控制增長函數”,在以下四個函數中:①
是“控制增長函數”,在以下四個函數中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增長函數”的有( )
.是“控制增長函數”的有( )
A.②③B.③④C.②③④D.①②④
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,…,
,…,![]() 是由
是由![]() (
(![]() )個整數
)個整數![]() ,
,![]() ,…,
,…,![]() 按任意次序排列而成的數列,數列
按任意次序排列而成的數列,數列![]() 滿足
滿足![]() (
(![]() ),
),![]() ,
,![]() ,…,
,…,![]() 是
是![]() ,
,![]() ,…,
,…,![]() 按從大到小的順序排列而成的數列,記
按從大到小的順序排列而成的數列,記![]() .
.
(1)證明:當![]() 為正偶數時,不存在滿足
為正偶數時,不存在滿足![]() (
(![]() )的數列
)的數列![]() .
.
(2)寫出![]() (
(![]() ),并用含
),并用含![]() 的式子表示
的式子表示![]() .
.
(3)利用![]() ,證明:
,證明:![]() 及
及![]() .(參考:
.(參考:![]() .)
.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公比大于
是公比大于![]() 的等比數列,
的等比數列,![]() 為數列
為數列![]() 的前
的前![]() 項和,
項和,![]() ,且
,且![]() ,
,![]() ,
,![]() 成等差數列.數列
成等差數列.數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() 滿足
滿足![]() ,且
,且![]() ,
,
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)令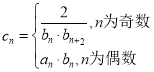 ,求數列
,求數列![]() 的前
的前![]() 項和為
項和為![]() ;
;
(3)將數列![]() ,
,![]() 的項按照“當
的項按照“當![]() 為奇數時,
為奇數時,![]() 放在前面;當
放在前面;當![]() 為偶數時,
為偶數時,![]() 放在前面”的要求進行排列,得到一個新的數列:
放在前面”的要求進行排列,得到一個新的數列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,求這個新數列的前
,求這個新數列的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為棱
為棱![]() 上的點,且
上的點,且![]() .
.
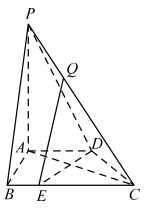
(1)求證:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)設![]() 為棱
為棱![]() 上的點(不與
上的點(不與![]() ,
,![]() 重合),且直線
重合),且直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】用一個長為![]() ,寬為
,寬為![]() 的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
的矩形鐵皮(如圖1)制作成一個直角圓形彎管(如圖3):先在矩形的中間畫一條曲線,并沿曲線剪開,將所得的兩部分分別卷成體積相等的斜截圓柱狀(如圖2),然后將其中一個適當翻轉拼接成直角圓形彎管(如圖3)(不計拼接損耗部分),并使得直角圓形彎管的體積最大;
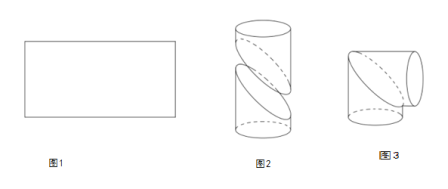
(1)求直角圓形彎管(圖3)的體積;
(2)求斜截面橢圓的焦距;
(3)在相應的圖1中建立適當的坐標系,使所畫的曲線的方程為![]() ,求出方程并畫出大致圖像;
,求出方程并畫出大致圖像;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數方程為:
,直線l的參數方程為:![]() (t為參數),直線l與曲線C分別交于
(t為參數),直線l與曲線C分別交于![]() 兩點.
兩點.
(1)寫出曲線C和直線l的普通方程;
(2)若點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)若動點![]() 為
為![]() 外一點,且
外一點,且![]() 到
到![]() 的兩條切線相互垂直,求
的兩條切線相互垂直,求![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設![]() 的另一個焦點為
的另一個焦點為![]() ,過
,過![]() 上一點
上一點![]() 的切線與(2)所求軌跡
的切線與(2)所求軌跡![]() 交于點
交于點![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com