
【題目】已知橢圓![]() :
:![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)若動點![]() 為
為![]() 外一點,且
外一點,且![]() 到
到![]() 的兩條切線相互垂直,求
的兩條切線相互垂直,求![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設![]() 的另一個焦點為
的另一個焦點為![]() ,過
,過![]() 上一點
上一點![]() 的切線與(2)所求軌跡
的切線與(2)所求軌跡![]() 交于點
交于點![]() ,
,![]() ,求證:
,求證:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)見解析.
;(3)見解析.
【解析】
(1)利用題中條件求出![]() 的值,然后根據離心率求出
的值,然后根據離心率求出![]() 的值,最后根據
的值,最后根據![]() 三者的關系求出
三者的關系求出![]() 的值,從而確定橢圓C的標準方程;
的值,從而確定橢圓C的標準方程;
(2)設![]() ,切點分別為
,切點分別為![]() ,
,![]() ,當
,當![]() 時,設切線方程為
時,設切線方程為![]() ,與橢圓聯立消去
,與橢圓聯立消去![]() ,得
,得![]() ,根據根的判別式
,根據根的判別式![]() ,化簡得
,化簡得![]() ,又因為
,又因為![]() 在橢圓
在橢圓![]() 外,
外, ![]() .又因為
.又因為![]() ,所以
,所以![]() ,即
,即![]() ,化簡為
,化簡為![]() ,
,
整理即可得![]() 的軌跡方程.
的軌跡方程.
(3)設![]() ,先求
,先求![]() .方法一:由相交弦定理,得
.方法一:由相交弦定理,得![]() .
.
方法二:切線![]() 的參數方程,將
的參數方程,將![]() 代入圓
代入圓![]() ,因為點
,因為點![]() 在圓
在圓![]() 內,整理可得
內,整理可得![]() .再利用公式求
.再利用公式求![]() ,所以
,所以![]() 證得.
證得.
(1)解:設![]() ,
,
由題設,得![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() 的標準方程為
的標準方程為![]() .
.
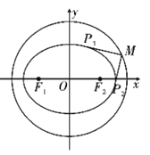
(2)解:如圖,設![]() ,切點分別為
,切點分別為![]() ,
,![]() ,
,
當![]() 時,設切線方程為
時,設切線方程為![]() ,
,
聯立方程,得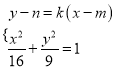 ,
,
消去![]() ,得
,得![]() ,①
,①
關于![]() 的方程①的判別式
的方程①的判別式![]() ,
,
化簡,得![]() ,②
,②
關于![]() 的方程②的判別式
的方程②的判別式![]()
![]() ,
,
因為![]() 在橢圓
在橢圓![]() 外,
外,
所以![]() ,即
,即![]() ,所以
,所以![]() .
.
關于![]() 的方程②有兩個實根
的方程②有兩個實根![]() ,
,![]() 分別是切線
分別是切線![]() ,
,![]() 的斜率,
的斜率,
因為![]() ,所以
,所以![]() ,即
,即![]() ,化簡為
,化簡為![]() ,
,
當![]() 時,可得
時,可得![]() ,滿足
,滿足![]() ,
,
所以![]() 的軌跡方程為
的軌跡方程為![]() .
.
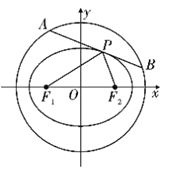
(3)證明:如圖,設![]() ,先求
,先求![]() .
.
方法一:由相交弦定理,得
![]() .
.
方法二:切線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),
![]() ,
,
代入圓![]() ,整理得
,整理得![]() ,
,
因為點![]() 在圓
在圓![]() 內,
內,
所以上述方程必有兩個不等實根![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
所以![]()
![]() ,
,
當![]() 時,
時,![]() ,仍有
,仍有![]() .
.
再求![]() .
.
![]()
![]()
![]()
![]() ,
,
因為點![]() 在橢圓
在橢圓![]() 上,所以
上,所以![]() ,即
,即![]() ,
,
所以![]() ,
,
所以![]() .
.


科目:高中數學 來源: 題型:
【題目】對于定義在![]() 上的函數
上的函數![]() ,若存在正常數
,若存在正常數![]() 、
、![]() ,使得
,使得![]() 對一切
對一切![]() 均成立,則稱
均成立,則稱![]() 是“控制增長函數”,在以下四個函數中:①
是“控制增長函數”,在以下四個函數中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增長函數”的有( )
.是“控制增長函數”的有( )
A.②③B.③④C.②③④D.①②④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】追求人類與生存環境的和諧發展是中國特色社會主義生態文明的價值取向.為了改善空氣質量,某城市環保局隨機抽取了一年內100天的空氣質量指數(![]() )的檢測數據,結果統計如下:
)的檢測數據,結果統計如下:
|
|
|
|
|
|
|
空氣質量 | 優 | 良 | 輕度污染 | 中度污染 | 重度污染 | 嚴重污染 |
天數 | 6 | 14 | 18 | 27 | 25 | 10 |
(1)從空氣質量指數屬于![]() ,
,![]() 的天數中任取3天,求這3天中空氣質量至少有2天為優的概率;
的天數中任取3天,求這3天中空氣質量至少有2天為優的概率;
(2)已知某企業每天的經濟損失![]() (單位:元)與空氣質量指數
(單位:元)與空氣質量指數![]() 的關系式為
的關系式為 ,試估計該企業一個月(按30天計算)的經濟損失的數學期望.
,試估計該企業一個月(按30天計算)的經濟損失的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】3個紅球與3個黑球隨機排成一行,從左到右依次在球上標記1,2,3,4,5,6,則紅球上的數字之和小于黑球上的數字之和的概率為( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某生產旅游紀念品的工廠,擬在2017年度進行系列促銷活動.經市場調查和測算,該紀念品的年銷售量x(單位:萬件)與年促銷費用t(單位:萬元)之間滿足3-x與t+1成反比例.若不搞促銷活動,紀念品的年銷售量只有1萬件.已知工廠2017年生產紀念品的固定投資為3萬元,每生產1萬件紀念品另外需要投資32萬元.當工廠把每件紀念品的售價定為“年平均每件生產成本的1.5倍”與“年平均每件所占促銷費的一半”之和時,則當年的產量和銷量相等.(利潤=收入-生產成本-促銷費用)
(1)請把該工廠2017年的年利潤y(單位:萬元)表示成促銷費t(單位:萬元)的函數;
(2)試問:當2017年的促銷費投入多少萬元時,該工廠的年利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了了解居民的家庭收人情況,某社區組織工作人員從該社區的居民中隨機抽取了![]() 戶家庭進行問卷調查.經調查發現,這些家庭的月收人在
戶家庭進行問卷調查.經調查發現,這些家庭的月收人在![]() 元到
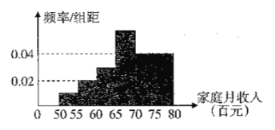
元到![]() 元之間,根據統計數據作出如圖所示的頻率分布直方圖.已知圖中從左至右第一 、二、四小組的頻率之比為
元之間,根據統計數據作出如圖所示的頻率分布直方圖.已知圖中從左至右第一 、二、四小組的頻率之比為![]() ,且第四小組的頻數為
,且第四小組的頻數為![]() .
.
(1)求![]() ;
;
(2)求這![]() 戶家庭月收人的眾數與中位數(結果精確到
戶家庭月收人的眾數與中位數(結果精確到![]() );
);
(3)這![]() 戶家庭月收入在第一、二、三小組的家庭中,用分層抽樣的方法任意抽取
戶家庭月收入在第一、二、三小組的家庭中,用分層抽樣的方法任意抽取![]() 戶家庭,并從這
戶家庭,并從這![]() 戶家庭中隨機抽取
戶家庭中隨機抽取![]() 戶家庭進行慰問,求這
戶家庭進行慰問,求這![]() 戶家庭月收入都不超過
戶家庭月收入都不超過![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】幾位大學生響應國家的創業號召,開發了一款應用軟件,為激發大家的學習興趣,他們推出了“解數學題獲取軟件激活碼”的活動,這款軟件的激活碼為下列數學問題的答案:已知數列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一項是![]() ,接下來的兩項是
,接下來的兩項是![]() ,再接下來的三項是
,再接下來的三項是![]() ,……,以此類推,求滿足如下條件的最小整數
,……,以此類推,求滿足如下條件的最小整數![]() 且該數列的前
且該數列的前![]() 項和為2的整數冪,那么該軟件的激活碼是________。
項和為2的整數冪,那么該軟件的激活碼是________。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() :
:![]() 過點
過點![]() ,
,![]() 為其焦點,過
為其焦點,過![]() 且不垂直于
且不垂直于![]() 軸的直線
軸的直線![]() 交拋物線
交拋物線![]() 于
于![]() ,
,![]() 兩點,動點
兩點,動點![]() 滿足
滿足![]() 的垂心為原點
的垂心為原點![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)求證:動點![]() 在定直線
在定直線![]() 上,并求
上,并求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com