
【題目】幾位大學(xué)生響應(yīng)國家的創(chuàng)業(yè)號召,開發(fā)了一款應(yīng)用軟件,為激發(fā)大家的學(xué)習(xí)興趣,他們推出了“解數(shù)學(xué)題獲取軟件激活碼”的活動,這款軟件的激活碼為下列數(shù)學(xué)問題的答案:已知數(shù)列1、1、2、1、2、4、8、1、2、4、8、16、……,其中第一項是![]() ,接下來的兩項是
,接下來的兩項是![]() ,再接下來的三項是
,再接下來的三項是![]() ,……,以此類推,求滿足如下條件的最小整數(shù)
,……,以此類推,求滿足如下條件的最小整數(shù)![]() 且該數(shù)列的前
且該數(shù)列的前![]() 項和為2的整數(shù)冪,那么該軟件的激活碼是________。
項和為2的整數(shù)冪,那么該軟件的激活碼是________。
【答案】![]()
【解析】
由題意先將此數(shù)列分組,再求得前![]() 組的項之和為
組的項之和為![]()
![]() 及項數(shù),由題意可知
及項數(shù),由題意可知![]() 為2的整數(shù)冪,只需將
為2的整數(shù)冪,只需將![]() 消去即可,再分別討論即可得解.
消去即可,再分別討論即可得解.
解:由題意可知,將1、1、2、1、2、4、8、1、2、4、8、16、……,可分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,
根據(jù)等比數(shù)列前![]() 項和公式,求得每組和分別為
項和公式,求得每組和分別為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
每組含有的項數(shù)為:![]() ,總共的項數(shù)為
,總共的項數(shù)為![]() ,
,
所有組的項之和為![]()
![]()
![]()
![]()
![]()
![]() ,由題意可知:
,由題意可知:![]() 為2的整數(shù)冪,只需將
為2的整數(shù)冪,只需將![]() 消去即可,
消去即可,
則①![]() ,解得
,解得![]() ,總共有
,總共有![]() 項,不滿足
項,不滿足![]() ,
,
②![]() ,解得
,解得![]() ,總共有
,總共有![]() 項,不滿足
項,不滿足![]() ,
,
③![]() ,解得
,解得![]() ,總共有
,總共有![]() 項,不滿足
項,不滿足![]() ,
,
④![]() ,解得
,解得![]() ,總共有
,總共有![]() 項,滿足
項,滿足![]() ,
,
即該軟件的激活碼是![]() ,
,
故答案為:![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標系中,以原點為極點,x軸的正半軸為極軸建立極坐標系,已知曲線![]() ,直線l的參數(shù)方程為:
,直線l的參數(shù)方程為:![]() (t為參數(shù)),直線l與曲線C分別交于
(t為參數(shù)),直線l與曲線C分別交于![]() 兩點.
兩點.
(1)寫出曲線C和直線l的普通方程;
(2)若點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓![]() :
:![]() 的一個焦點為
的一個焦點為![]() ,離心率為
,離心率為![]() .
.
(1)求![]() 的標準方程;
的標準方程;
(2)若動點![]() 為
為![]() 外一點,且
外一點,且![]() 到
到![]() 的兩條切線相互垂直,求
的兩條切線相互垂直,求![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)設(shè)![]() 的另一個焦點為
的另一個焦點為![]() ,過
,過![]() 上一點
上一點![]() 的切線與(2)所求軌跡
的切線與(2)所求軌跡![]() 交于點
交于點![]() ,
,![]() ,求證:
,求證:![]() .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在圓臺![]() 中,平面
中,平面![]() 過上下底面的圓心
過上下底面的圓心![]() ,
,![]() ,點M在
,點M在![]() 上,N為
上,N為![]() 的中點,
的中點,![]() .
.
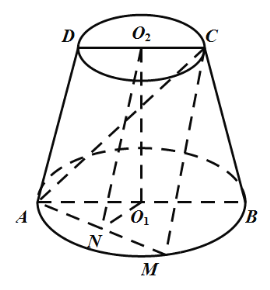
(1)求證:平面![]() 平面
平面![]() ;
;
(2)當![]() 時,
時,![]() 與底面
與底面![]() 所成角的正弦值為
所成角的正弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,且
,且![]() 在
在![]() 上存在零點,求實數(shù)
上存在零點,求實數(shù)![]() 的取值范圍;
的取值范圍;
(2)若對任意![]() ,存在
,存在![]() 使
使![]() ,求實數(shù)
,求實數(shù)![]() 的取值范圍;
的取值范圍;
(3)若存在實數(shù)![]() ,使得當
,使得當![]() 時,
時,![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,![]() 是一個三棱錐,
是一個三棱錐,![]() 是圓的直徑,
是圓的直徑,![]() 是圓上的點,
是圓上的點,![]() 垂直圓所在的平面,
垂直圓所在的平面,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 的中點.
的中點.
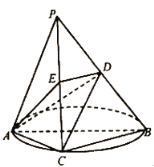
(1)求證:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于函數(shù)![]() ,若存在正常數(shù)
,若存在正常數(shù)![]() ,使得對任意的
,使得對任意的![]() ,都有
,都有![]() 成立,我們稱函數(shù)
成立,我們稱函數(shù)![]() 為“
為“![]() 同比不減函數(shù)”.
同比不減函數(shù)”.
(1)求證:對任意正常數(shù)![]() ,
,![]() 都不是“
都不是“![]() 同比不減函數(shù)”;
同比不減函數(shù)”;
(2)若函數(shù)![]() 是“
是“![]() 同比不減函數(shù)”,求
同比不減函數(shù)”,求![]() 的取值范圍;
的取值范圍;
(3)是否存在正常數(shù)![]() ,使得函數(shù)
,使得函數(shù)![]() 為“
為“![]() 同比不減函數(shù)”,若存在,求
同比不減函數(shù)”,若存在,求![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{bn}的前n項和為Tn,且T4=4,b5=6.
(1)求數(shù)列{bn}的通項公式;
(2)若正整數(shù)n1,n2,…,nt,…滿足5<n1<n2<…<nt,…且b3,b5,![]() ,
,![]() ,…,
,…,![]() ,…成等比數(shù)列,求數(shù)列{nt}的通項公式(t是正整數(shù));
,…成等比數(shù)列,求數(shù)列{nt}的通項公式(t是正整數(shù));
(3)給出命題:在公比不等于1的等比數(shù)列{an}中,前n項和為Sn,若am,am+2,am+1成等差數(shù)列,則Sm,Sm+2,Sm+1也成等差數(shù)列.試判斷此命題的真假,并證明你的結(jié)論.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com