日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 高中數學 > 題目詳情
4．不等式（a-3）x2+2（a-3）x-4＜0對于一切x∈R恒成立，那么a的取值范圍是（　　）
A．（-∞，-3）B．（-1，3]C．（-∞，-3]D．（-3，3]

分析 當a=3時不等式即為-4＜0，對一切x∈R恒成立，當a≠3時 利用二次函數的性質列出a滿足的條件并計算，最后兩部分的合并即為所求范圍．

解答 解：當a-3=0，a=3時不等式即為-4＜0，對一切x∈R恒成立 ①
當a≠3時，則須$\left\{\begin{array}{l}{a-3＜0}\\{△=4（a-3）^{2}+16（a-3）＜0}\end{array}\right.$，解得：$\left\{\begin{array}{l}{a＜3}\\{-1＜a＜3}\end{array}\right.$，
∴-1＜a＜3 ②
由①②得實數a的取值范圍是（-1，3]．
故選：B．

點評 本題考查不等式恒成立的參數取值范圍，考查二次函數的性質．注意對二次項系數是否為0進行討論．

練習冊系列答案
相關習題

科目：高中數學 來源： 題型：選擇題

14．已知正方形的邊長為1，$\overrightarrow{AB}=\overrightarrow a，\overrightarrow{BC}=\overrightarrow b，\overrightarrow{AC}=\overrightarrow c$，則$|{\overrightarrow a+\overrightarrow b+\overrightarrow c}|$等于（　　）
A．0B．3C．$\sqrt{2}$D．$2\sqrt{2}$

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

15．在直角坐標系xOy中，曲線C1：$\left\{{\begin{array}{l}{x=3+αcost}\\{y=2+αsint}\end{array}}\right.$（t為參數，a＞0），在以坐標原點為極點，x軸的非負半軸為極軸的極坐標系中，曲線C2：ρ=4sinθ．
（1）試將曲線C1與C2化為直角坐標系xOy中的普通方程，并指出兩曲線有公共點時a的取值范圍；
（2）當a=3時，兩曲線相交于A，B兩點，求|AB|的值．

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

12．設a=log0.80.9，b=log1.10.9，c=1.10.9，則a，b，c的大小關系為（　　）
A．b＜a＜cB．a＜c＜bC．a＜b＜cD．c＜a＜b

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

19．將y=cosx的圖象上的所有點的縱坐標不變，橫坐標縮小到原來的一半，然后再將所得圖象向左平移$\frac{π}{4}$個單位長度，則最后所得圖象的解析式為（　　）
A．y=cos（2x+$\frac{π}{4}$）B．y=cos（$\frac{x}{2}$+$\frac{π}{4}$）C．y=sin2xD．y=-sin2x

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

9．設函數$f（x）=\left\{\begin{array}{l}x-[x]，x≥0\\ f（x+1）\;，x＜0\end{array}\right.$其中[x]表示不超過x的最大整數如[-1.5]=-2，[2.5]=2，若直線y=k（x-1）（k＜0）與函數y=f（x）的圖象只有三個不同的交點，則k的取值范圍為（　　）
A．$[-\frac{1}{2}，-\frac{1}{3}]$B．$（-\frac{1}{2}，-\frac{1}{3}）$C．$（-1，-\frac{1}{2}]$D．$（-1，-\frac{1}{2}）$

查看答案和解析>>

科目：高中數學 來源： 題型：選擇題

16．要得到函數y=sin$\frac{1}{2}$x的圖象，只需將函數y=sin（$\frac{1}{2}$x+$\frac{π}{6}$）的圖象（　　）
A．向左平移$\frac{π}{3}$個單位B．向右平移$\frac{π}{3}$個單位
C．向左平移$\frac{π}{6}$個單位D．向右平移$\frac{π}{6}$個單位

查看答案和解析>>

科目：高中數學 來源： 題型：填空題

13．已知a＞0，b＞0，且$\sqrt{3}$是3a與3b的等比中項，若$\frac{1}{a}$+$\frac{4}{b}$≥2m2+3m恒成立，則實數m的取值范圍是[-3，$\frac{3}{2}$]．

查看答案和解析>>

科目：高中數學 來源： 題型：解答題

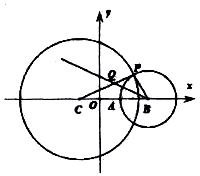8．如圖，在平面直角坐標系xoy中，已知圓C：（x+1）2+y2=16，點A（1，0），點B（a，0）（|a|＞3），以B為圓心，|BA|的半徑作圓，交圓C于點P，且的∠PBA的平分線次線段CP于點Q．
（I）當a變化時，點Q始終在某圓錐曲線τ是運動，求曲線τ的方程；
（II）已知直線l過點C，且與曲線τ交于M、N兩點，記△OCM面積為S1，△OCN面積為S2，求$\frac{S_1}{S_2}$的取值范圍．

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 亚洲第一黄色 | 国产成人a亚洲精品 | 91视频在线免费观看 | 日韩成人免费视频 | 精品伊人久久 | 国产自产21区 | 欧美一级精品 | 中文字幕在线观看一区二区 | 亚洲午夜在线观看 | 蜜桃91丨九色丨蝌蚪91桃色 | 欧美一级大片 | 性生活视频网站 | 国产在线第一页 | 国产精品久久久久久99 | 黄免费视频 | 久久精品久久久久久久 | 触手繁殖の地狱3d啪啪 | 国产精品国产三级国产aⅴ浪潮 | 伊人久久中文字幕 | 日韩视频免费大全中文字幕 | 久久久国产一区二区三区 | 成年人免费看视频 | 欧美日韩黄色片 | 日日夜夜人人 | 日韩一级黄 | 欧洲一级片 | 成人免费黄色片 | 日韩毛片在线播放 | 亚洲深夜福利 | 日韩一区二区三区在线播放 | 国产无遮挡又黄又爽又色 | 又黄又爽的免费视频 | 九九精品视频在线观看 | www一区| 日韩免费网站 | 丁香午夜 | 在线播放一区 | 一区视频在线 | 国内精品国产成人国产三级 | 91一区二区 | 午夜免费福利 |