
 ,去參加乙游戲的概率為
,去參加乙游戲的概率為 .…(2分)
.…(2分)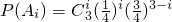 .…(3分)
.…(3分) .…(5分)
.…(5分)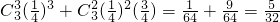 .
. .…(7分)
.…(7分)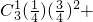
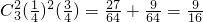 ,…(9分)P(ξ=3)=P(A0)+P(A3)=
,…(9分)P(ξ=3)=P(A0)+P(A3)=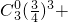
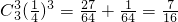 .…(10分)
.…(10分)| ξ | 1 | 3 |
| P |  |  |
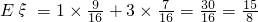 .…(12分)
.…(12分)

 中考利劍中考試卷匯編系列答案
中考利劍中考試卷匯編系列答案 教育世家狀元卷系列答案
教育世家狀元卷系列答案科目:高中數學 來源: 題型:填空題
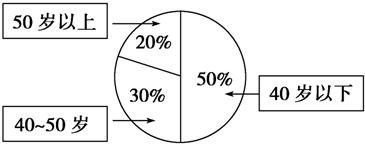 某單位200名職工的年齡分布情況如圖,現要從中抽取40名職工作樣本、用系統抽樣法,將全體職工隨機按1~200編號,并按編號順序平均分為40組(1~5號,6~10號,…,196~200號).若第5組抽出的號碼為22,則第8組抽出的號碼應是________.若用分層抽樣方法,則40歲以下年齡段應抽取________人.
某單位200名職工的年齡分布情況如圖,現要從中抽取40名職工作樣本、用系統抽樣法,將全體職工隨機按1~200編號,并按編號順序平均分為40組(1~5號,6~10號,…,196~200號).若第5組抽出的號碼為22,則第8組抽出的號碼應是________.若用分層抽樣方法,則40歲以下年齡段應抽取________人.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
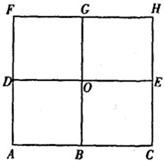 某城市有連接8個小區A、B、C、D、E、F、G、H和市中心O的整齊方格形道路網,每個小方格均為正方形,如圖.某人從道路網中隨機地選擇一條最短路徑,由小區A前往H.
某城市有連接8個小區A、B、C、D、E、F、G、H和市中心O的整齊方格形道路網,每個小方格均為正方形,如圖.某人從道路網中隨機地選擇一條最短路徑,由小區A前往H.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com