
| A. | y=$\frac{x}{x+1}$ | B. | y=1-x | C. | y=x2-x | D. | y=1-x2 |
分析 利用導數法,逐一分析給定四個函數在區(qū)間(0,+∞)上的單調性,可得結論.
解答 解:函數y=$\frac{x}{x+1}$的導函數y′=$\frac{1}{(x+1)^{2}}$,在區(qū)間(0,+∞)上,y′>0恒成立,故函數在區(qū)間(0,+∞)上單調遞增;
函數y=1-x的導函數y′=-1,在區(qū)間(0,+∞)上,y′<0恒成立,故函數在區(qū)間(0,+∞)上單調遞減;
函數y=x2-x的導函數y′=2x-1,在區(qū)間(0,$\frac{1}{2}$)上,y′<0恒成立,故函數在區(qū)間(0,+∞)上不單調遞增;
函數y=1-x2的導函數y′=-2x,在區(qū)間(0,+∞)上,y′<0恒成立,故函數在區(qū)間(0,+∞)上單調遞減;
故選A.
點評 本題考查的知識點是利用導數研究函數的單調性,難度中檔.


 培優(yōu)口算題卡系列答案
培優(yōu)口算題卡系列答案 開心口算題卡系列答案
開心口算題卡系列答案 口算題卡河北少年兒童出版社系列答案
口算題卡河北少年兒童出版社系列答案科目:高中數學 來源: 題型:解答題
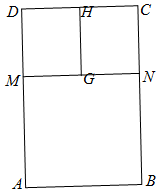 擬用長度為l的鋼筋焊接一個如圖所示的矩形框架結構(鋼筋體積、焊接點均忽略不計),其中G、H分別為框架梁MN、CD的中點,MN∥CD,設框架總面積為S平方米,BN=2CN=2x米.
擬用長度為l的鋼筋焊接一個如圖所示的矩形框架結構(鋼筋體積、焊接點均忽略不計),其中G、H分別為框架梁MN、CD的中點,MN∥CD,設框架總面積為S平方米,BN=2CN=2x米.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{2016}{2017}$ | B. | $\frac{2017}{2016}$ | C. | $\frac{2015}{2017}$ | D. | $\frac{2015}{2016}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{4}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com