
【題目】已知f(x)為二次函數,且![]() .
.
(1)求f(x)的表達式;
(2)判斷函數![]() 在(0,+∞)上的單調性,并證明.
在(0,+∞)上的單調性,并證明.
【答案】(1)![]() ;(2)增函數,證明見解析.
;(2)增函數,證明見解析.
【解析】
(1)利用題中所給的條件,先設出函數的解析式,利用![]() ,將式子化為恒等式,利用對應項系數相等,得到方程組,求得結果;
,將式子化為恒等式,利用對應項系數相等,得到方程組,求得結果;
(2)先化簡函數解析式,利用單調性的定義,證明得到函數的單調性,得到結果.
(1)設f(x)=ax2+bx+c(a≠0),
由條件得:a(x+1)2+b(x+1)+c+a(x﹣1)2+b(x﹣1)+c=2x2﹣4x,
從而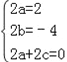 , 解得:
, 解得: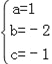 ,
,
所以f(x)=x2﹣2x﹣1;
(2)函數g(x)=![]() 在(0,+∞)上單調遞增.
在(0,+∞)上單調遞增.
理由如下:g(x)=![]() =
=![]() ,
,
設設任意x1,x2∈(0,+∞),且x1<x2,
則g(x1)﹣g(x2)=![]() ﹣(
﹣(![]() )=(x1﹣x2)(1+
)=(x1﹣x2)(1+![]() ),
),
∵x1,x2∈(0,+∞),且x1<x2,
∴x1﹣x2<0,1+![]() >0,
>0,
∴g(x1)﹣g(x2)<0,即g(x1)<g(x2),
所以函數g(x)=![]() 在(0,+∞)上單調遞增.
在(0,+∞)上單調遞增.


科目:高中數學 來源: 題型:
【題目】某地某路無人駕駛公交車發車時間間隔![]() (單位:分鐘)滿足
(單位:分鐘)滿足![]() ,
,![]() .經測算,該路無人駕駛公交車載客量
.經測算,該路無人駕駛公交車載客量![]() 與發車時間間隔
與發車時間間隔![]() 滿足:
滿足: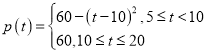 ,其中
,其中![]() .
.
(1)求![]() ,并說明
,并說明![]() 的實際意義;
的實際意義;
(2)若該路公交車每分鐘的凈收益![]() (元),問當發車時間間隔為多少時,該路公交車每分鐘的凈收益最大?并求每分鐘的最大凈收益.
(元),問當發車時間間隔為多少時,該路公交車每分鐘的凈收益最大?并求每分鐘的最大凈收益.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐,規定:每場知識競賽前三名的得分都分別為![]()
![]() 且
且![]() ;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為
;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分![]() 為
為![]()
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
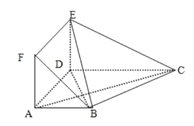
【題目】在多面體![]() 中,底面
中,底面![]() 是梯形,四邊形
是梯形,四邊形![]() 是正方形,
是正方形,![]() ,
,![]() ,面
,面![]() 面
面![]() ,
,![]() .
.![]() .
.
(1)求證:平面![]() 平面
平面![]() ;
;
(2)設![]() 為線段
為線段![]() 上一點,
上一點,![]() ,試問在線段
,試問在線段![]() 上是否存在一點
上是否存在一點![]() ,使得
,使得![]() 平面
平面![]() ,若存在,試指出點
,若存在,試指出點![]() 的位置;若不存在,說明理由?
的位置;若不存在,說明理由?
(3)在(2)的條件下,求點![]() 到平面
到平面![]() 的距離.
的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了鼓勵節約用電,遼寧省實行階梯電價制度,其中每戶的用電單價與戶年用電量的關系如下表所示.
分檔 | 戶年用電量(度) | 用電單價(元/度) |
第一階梯 |
| 0.5 |
第二階梯 |
| 0.55 |
第三階梯 |
| 0.80 |
記用戶年用電量為![]() 度時應繳納的電費為
度時應繳納的電費為![]() 元.
元.
(1)寫出![]() 的解析式;
的解析式;
(2)假設居住在沈陽的范偉一家2018年共用電3000度,則范偉一家2018年應繳納電費多少元?
(3)居住在大連的張莉一家在2018年共繳納電費1942元,則張莉一家在2018年用了多少度電?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年1月31日晚上月全食的過程分為初虧、食既、食甚、生光、復圓五個階段,月食的初虧發生在19時48分,20時51分食既,食甚時刻為21時31分,22時08分生光,直至23時12分復圓.全食伴隨有藍月亮和紅月亮,全食階段的“紅月亮”將在食甚時刻開始,生光時刻結東,一市民準備在19:55至21:56之間的某個時刻欣賞月全食,則他等待“紅月亮”的時間不超過30分鐘的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com