
【題目】已知函數![]()
![]() ,
,
(1)求當![]() 在
在![]() 處的切線的斜率最小時,
處的切線的斜率最小時,![]() 的解析式;
的解析式;
(2)在(1)的條件下,是否總存在實數m,使得對任意的![]() ,總存在
,總存在![]() ,使得
,使得![]() 成立?若存在,求出實數m的取值范圍;若不存在,說明理由.
成立?若存在,求出實數m的取值范圍;若不存在,說明理由.
科目:高中數學 來源: 題型:
【題目】某社區![]() 名居民參加
名居民參加![]() 年國慶活動,他們的年齡在
年國慶活動,他們的年齡在![]() 歲至
歲至![]() 歲之間,將年齡按
歲之間,將年齡按![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分組,得到的頻率分布直方圖如圖所示.
分組,得到的頻率分布直方圖如圖所示.
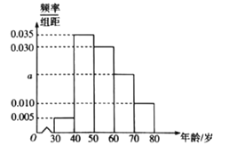
(1)求![]() 的值,并求該社區參加
的值,并求該社區參加![]() 年國慶活動的居民的平均年齡(每個分組取中間值作代表);
年國慶活動的居民的平均年齡(每個分組取中間值作代表);
(2)現從年齡在![]() 、
、![]() 的人員中按分層抽樣的方法抽取
的人員中按分層抽樣的方法抽取![]() 人,再從這
人,再從這![]() 人中隨機抽取
人中隨機抽取![]() 人進行座談,用
人進行座談,用![]() 表示參與座談的居民的年齡在
表示參與座談的居民的年齡在![]() 的人數,求
的人數,求![]() 的分布列和數學期望;
的分布列和數學期望;
(3)若用樣本的頻率代替概率,用隨機抽樣的方法從該地![]() 歲至
歲至![]() 歲之間的市民中抽取
歲之間的市民中抽取![]() 名進行調查,其中有
名進行調查,其中有![]() 名市民的年齡在
名市民的年齡在![]() 的概率為
的概率為![]() ,當
,當![]() 最大時,求
最大時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】根據閱兵領導小組辦公室介紹,2019年國慶70周年閱兵有59個方(梯)隊和聯合軍樂團,總規模約1.5萬人,是近幾次閱兵中規模最大的一次.其中,徒步方隊15個.為了保證閱兵式時隊列保持整齊,各個方隊對受閱隊員的身高也有著非常嚴格的限制,太高或太矮都不行.徒步方隊隊員,男性身高普遍在175cm至185cm之間;女性身高普遍在163cm至175cm之間,這是常規標準.要求最為嚴格的三軍儀仗隊,其隊員的身高一般都在184cm至190cm之間.經過隨機調查某個閱兵陣營中女子100人,得到她們身高的直方圖,如圖,記C為事件:“某一閱兵女子身高不低于169cm”,根據直方圖得到P(C)的估計值為0.5.
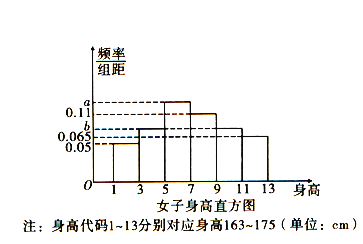
(1)求直方圖中a,b的值;
(2)估計這個陣營女子身高的平均值 (同一組中的數據用該組區間的中點值為代表)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在復平面內,給出以下四個說法:
①實軸上的點表示的數均為實數;
②虛軸上的點表示的數均為純虛數;
③互為共軛復數的兩個復數的實部相等,虛部互為相反數;
④已知復數![]() 滿足
滿足![]() ,則
,則![]() 在復平面內所對應的點位于第四象限.
在復平面內所對應的點位于第四象限.
其中說法正確的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】改革開放以來,人們的支付方式發生了巨大轉變.近年來,移動支付已成為主要支付方式之一.為了解某校學生上個月A,B兩種移動支付方式的使用情況,從全校學生中隨機抽取了100人,發現樣本中A,B兩種支付方式都不使用的有5人,樣本中僅使用A和僅使用B的學生的支付金額分布情況如下:
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
僅使用A | 18人 | 9人 | 3人 |
僅使用B | 10人 | 14人 | 1人 |
(Ⅰ)從全校學生中隨機抽取1人,估計該學生上個月A,B兩種支付方式都使用的概率;
(Ⅱ)從樣本僅使用A和僅使用B的學生中各隨機抽取1人,以X表示這2人中上個月支付金額大于1000元的人數,求X的分布列和數學期望;
(Ⅲ)已知上個月樣本學生的支付方式在本月沒有變化.現從樣本僅使用A的學生中,隨機抽查3人,發現他們本月的支付金額都大于2000元.根據抽查結果,能否認為樣本僅使用A的學生中本月支付金額大于2000元的人數有變化?說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校隨機抽取部分新生調查其上學所需時間(單位:分鐘),并將所得數據繪制成頻率分布直方圖(如圖).已知上學所需時間的范圍是![]() ,樣本數據分組為
,樣本數據分組為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方圖中x的值;
(2)如果上學所需時間在![]() 的學生可申請在學校住宿,請估計該校800名新生中有多少名學生可以申請住宿.
的學生可申請在學校住宿,請估計該校800名新生中有多少名學生可以申請住宿.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數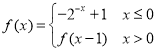 ,則下列命題中正確命題的個數是( )
,則下列命題中正確命題的個數是( )
①函數![]() 在
在![]() 上為周期函數
上為周期函數
②函數![]() 在區間
在區間![]() ,
,![]() 上單調遞增
上單調遞增
③函數![]() 在
在![]() (
(![]() )取到最大值
)取到最大值![]() ,且無最小值
,且無最小值
④若方程![]() (
(![]() )有且僅有兩個不同的實根,則
)有且僅有兩個不同的實根,則![]()
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知正三棱錐P-ABC的側面是直角三角形,PA=6,頂點P在平面ABC內的正投影為點D,D在平面PAB內的正投影為點E,連結PE并延長交AB于點G.

(Ⅰ)證明:G是AB的中點;
(Ⅱ)在圖中作出點E在平面PAC內的正投影F(說明作法及理由),并求四面體PDEF的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com