
| A. | f(x)=x3,x∈(-3,3) | B. | f(x)=tanx | C. | f(x)=x|x| | D. | $f(x)=ln{2^{{e^{-x}}-{e^x}}}$ |
分析 根據函數的奇偶性的定義,單調性的定義判斷,從而可得答案.
解答 解:A、∵f(x)=x3,定義域為(-3,3),
∴f(-x)=-f(x),x1<x2,則x13<x23,
∴f(x)=x3是奇函數又是增函數,不正確,
B、f(x)=tanx在定義域上不是減函數,不正確,
C、f(x)=x|x|=$\left\{\begin{array}{l}{{x}^{2},x≥0}\\{-{x}^{2},x<0}\end{array}\right.$,在定義域上不是減函數,不正確,
D、f(x)=(e-x-ex)ln2,f(-x)=(ex-e-x)ln2=-f(x),是奇函數,且在定義域上是減函數,正確,
故選D.
點評 本題考查了常見函數的單調性,奇偶性,注意定義域,單調區間的定義,屬于中檔題.


科目:高中數學 來源: 題型:選擇題
| A. | a>1 | B. | a<-1 | C. | a>2 | D. | a<-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
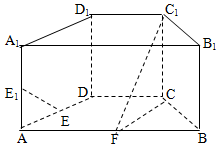 如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分別是棱AD、AA1、AB的中點.
如圖,在直四棱柱ABCD-A1B1C1D1中,底面ABCD為等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、E1、F分別是棱AD、AA1、AB的中點.查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
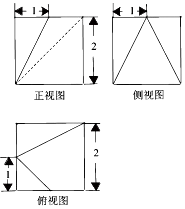
| A. | 8 | B. | 7 | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
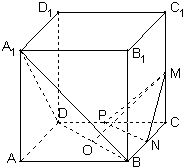 在單位正方體ABCD---A1B1C1D1中,M,N,P分別是CC1,BC,CD的中點,O為底面ABCD的中心.
在單位正方體ABCD---A1B1C1D1中,M,N,P分別是CC1,BC,CD的中點,O為底面ABCD的中心. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com