已知數(shù)列
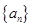
中,
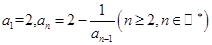
(1)求
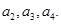
(2)試猜想
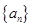
的通項公式,并用數(shù)學歸納法證明你的猜想。
(1)
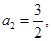
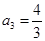
,
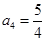
(2)猜想
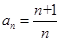
,嚴格按數(shù)學歸納法的步驟進行即可
試題分析:(1)由
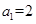
得
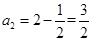
,
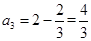
,
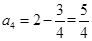
3分
(2)猜想
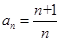
6分
證明:①當
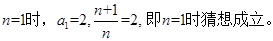
7分
②假設(shè)
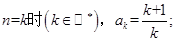
8分
則當
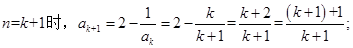
12分
即
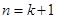
時猜想也成立。 13分
因此,由①②知猜想成立。 14分
點評:應用數(shù)學歸納法時,要嚴格遵守數(shù)學歸納法的證題步驟,尤其是第二步一定要用上歸納假設(shè),否則不是數(shù)學歸納法.
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
已知數(shù)列
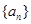
為等差數(shù)列,
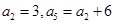
,數(shù)列
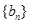
滿足
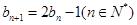
,且
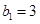
.(1)求通項公式
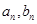
;(2)設(shè)數(shù)列
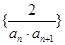
的前
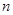
項和為
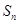
,試比較
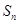
與
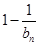
的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在等比數(shù)列
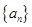
中,

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
等比數(shù)列{an}的前n項和為Sn,已知S1,S3,S2成等差數(shù)列,則公比q= .
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
設(shè)等比數(shù)列
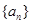
的公比
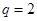
,前n項和為
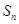
,則
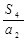
的值是( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
已知在等比數(shù)列
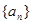
中,
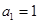
,且
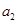
是
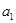
和
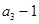
的等差中項.
(1)求數(shù)列
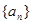
的通項公式;
(2)若數(shù)列
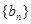
滿足
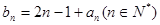
,求
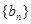
的前
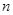
項和
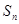
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
已知等比數(shù)列
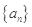
滿足
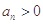
,
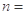
l,2,…,且
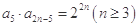
,則當
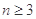
時,

.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
設(shè)各項均為正數(shù)的等比數(shù)列
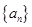
中,
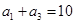
,
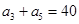
.設(shè)
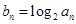
.
(1)求數(shù)列
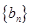
的通項公式;
(2)若
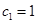
,
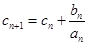
,求證:
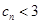
;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
an是實數(shù)構(gòu)成的等比數(shù)列,S
n=
a1+
a2+…+
an,則數(shù)列{S
n}中
| A.任一項均不為0 | B.必有一項為0 |
| C.至多有有限項為0 | D.或無一項為0,或無窮多項為0 |
查看答案和解析>>

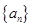 中,
中,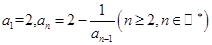
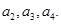 (2)試猜想
(2)試猜想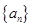 的通項公式,并用數(shù)學歸納法證明你的猜想。
的通項公式,并用數(shù)學歸納法證明你的猜想。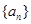 為等差數(shù)列,
為等差數(shù)列,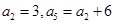 ,數(shù)列
,數(shù)列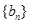 滿足
滿足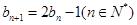 ,且
,且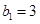 .(1)求通項公式
.(1)求通項公式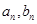 ;(2)設(shè)數(shù)列
;(2)設(shè)數(shù)列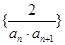 的前
的前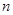 項和為
項和為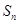 ,試比較
,試比較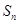 與
與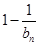 的大小.
的大小.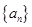 中,
中,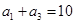 ,
,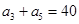 .設(shè)
.設(shè)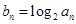 .
.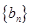 的通項公式;
的通項公式; 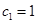 ,
,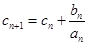 ,求證:
,求證: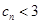 ;
;