Question

1．已知函數$f（x）=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0＜x≤e\\ x＞e\end{array}$，若正實數a，b，c互不相等，且f（a）=f（b）=f（c），則a+b+c的取值范圍為（　　）

• A． （e，2e+e²）
• B． $（\frac{1}{e}+2e，2+{e^2}）$
• C． $（\frac{1}{e}+e，2+{e^2}）$
• D． $（\frac{1}{e}+e，2e+{e^2}）$

Answer 1

分析 圖解法，畫出函數$f（x）=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0＜x≤e\\ x＞e\end{array}$的圖象，根據圖象分析可得a+b+c的取值范圍．

解答 解：如圖，畫出函數$f（x）=\left\{\begin{array}{l}|{lnx}|\\ 2-lnx\end{array}\right.$$\begin{array}{l}0＜x≤e\\ x＞e\end{array}$的圖象，
設a＜b＜c，則|lna|=|lnb|，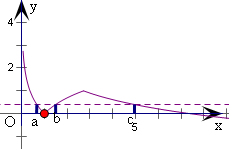
即有lna+lnb=0，即有ab=1，
當x＞e時，y=2-lnx遞減，
且與x軸交于（e²，0），
∴e＜c＜e²，
可得$\frac{1}{e}$＜a＜1，
當a趨近于$\frac{1}{e}$時，b，c趨近于e；
當a趨近于1時，b趨近于e，c趨近于e²，
可得a+b+c的取值范圍是（$\frac{1}{e}$+2e，2+e²）．
故選：B．

點評 此題是個中檔題．考查利用函數圖象分析解決問題的能力，以及對數函數圖象的特點，體現數形結合的思想．