
(14分)(2011•廣東)設b>0,數列{an}滿足a1=b,an=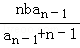 (n≥2)
(n≥2)
(1)求數列{an}的通項公式;
(2)證明:對于一切正整數n,2an≤bn+1+1.
(1)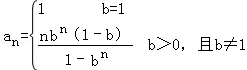 (2)見解析
(2)見解析
解析試題分析:(1)由題設形式可以看出,題設中給出了關于數列an的面的一個方程,即一個遞推關系,所以應該對此遞推關系進行變形整理以發(fā)現其中所蘊含的規(guī)律,觀察發(fā)現若對方程兩邊取倒數則可以得到一個類似等差數列的形式,對其中參數進行討論,分類求其通項即可.
(2)由于本題中條件較少,解題思路不宜用綜合法直接分析出,故求解本題可以采取分析法的思路,由結論探究其成立的條件,再證明此條件成立,即可達到證明不等式的目的.
解:(1)∵ (n≥2),
(n≥2),
∴ (n≥2),
(n≥2),
當b=1時,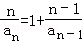 (n≥2),
(n≥2),
∴數列{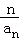 }是以
}是以 為首項,以1為公差的等差數列,
為首項,以1為公差的等差數列,
∴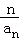 =1+(n﹣1)×1=n,即an=1,
=1+(n﹣1)×1=n,即an=1,
當b>0,且b≠1時, (n≥2),
(n≥2),
即數列{ }是以
}是以 =
=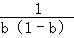 為首項,公比為
為首項,公比為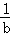 的等比數列,
的等比數列,
∴ =
=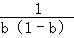 ×
× =
=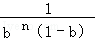 ,即an=
,即an= ,
,
∴數列{an}的通項公式是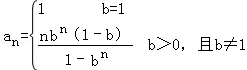
(2)證明:當b=1時,不等式顯然成立
當b>0,且b≠1時,an=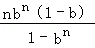 ,要證對于一切正整數n,2an≤bn+1+1,只需證2×
,要證對于一切正整數n,2an≤bn+1+1,只需證2×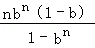 ≤bn+1+1,即證
≤bn+1+1,即證
∵
=
=(bn+1+1)×(bn﹣1+bn﹣2+…+b+1)
=(b2n+b2n﹣1+…+bn+2+bn+1)+(bn﹣1+bn﹣2+…+b+1)
=bn[(bn+bn﹣1+…+b2+b)+( +
+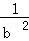 +…+
+…+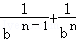 )]
)]
≥bn(2+2+…+2)=2nbn
所以不等式成立,
綜上所述,對于一切正整數n,有2an≤bn+1+1,
點評:本題考點是數列的遞推式,考查根據數列的遞推公式求數列的通項,研究數列的性質的能力,本題中遞推關系的形式適合用取倒數法將所給的遞推關系轉化為有規(guī)律的形式,兩邊取倒數,條件許可的情況下,使用此技巧可以使得解題思路呈現出來.數列中有請多成熟的規(guī)律,做題時要注意積累這些小技巧,在合適的情況下利用相關的技巧,可以簡化做題.在(2)的證明中,采取了分析法的來探究解題的思路,通過本題希望能進一步熟悉分析法證明問題的技巧.


 智慧課堂密卷100分單元過關檢測系列答案
智慧課堂密卷100分單元過關檢測系列答案 單元期中期末卷系列答案
單元期中期末卷系列答案科目:高中數學 來源: 題型:解答題
已知數列{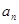 }是等差數列,其中每一項及公差
}是等差數列,其中每一項及公差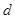 均不為零,設
均不為零,設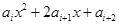 =0(
=0(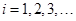 )是關于
)是關于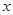 的一組方程.
的一組方程.
(1)求所有這些方程的公共根;
(2)設這些方程的另一個根為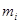 ,求證
,求證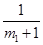 ,
,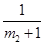 ,
,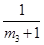 ,…,
,…, 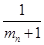 ,…也成等差數列.
,…也成等差數列.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com