
(12分)某算法的程序框圖如圖所示,其中輸入的變量x在1,2,3,…,24這24個整數中等可能隨機產生
(I)分別求出按程序框圖正確編程運行時輸出y的值為i的概率pi(i=1,2,3);
(II)甲乙兩同學依據自己對程序框圖的理解,各自編程寫出程序重復運行n次后,統計記錄輸出y的值為i(i=1,2,3)的頻數,以下是甲乙所作頻數統計表的部分數據.
甲的頻數統計圖(部分)
|
運行次數n |
輸出y的值為1的頻數 |
輸出y的值為2的頻數 |
輸出y的值為3的頻數 |
|
30 |
14 |
6 |
10 |
|
… |
… |
… |
… |
|
2100 |
1027 |
376 |
697 |
乙的頻數統計圖(部分)
|
運行次數n |
輸出y的值為1的頻數 |
輸出y的值為2的頻數 |
輸出y的值為3的頻數 |
|
30 |
12 |
11 |
7 |
|
… |
… |
… |
… |
|
2100 |
1051 |
696 |
353 |
當n=2100時,根據表中的數據,分別寫出甲、乙所編程序各自輸出y的值為i(i=1,2,3)的頻率(用分數表示),并判斷兩位同學中哪一位所編程序符合要求的可能系較大;
(III)將按程序擺圖正確編寫的程序運行3次,求輸出y的值為2的次數ξ的分布列及數學期望.

(I)輸出的y值為1的概率為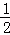 ,輸出的y值為2的概率為
,輸出的y值為2的概率為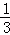 ,輸出的y值為3的概率為
,輸出的y值為3的概率為
(II)乙同學所編程序符合算法要求的可能性較大(III)1
【解析】(I)變量x是在1,2,3,…,24這24個整數中隨機產生的一個數,共有24種可能,
當x從1,3,5,7,9,11,13,15,17,19,21,23這12個數中產生時,輸出的y值為1,故P1=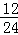 =
=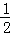 ;
;
當x從2,4,8,10,14,16,20,22這8個數中產生時,輸出的y值為2,故P2=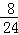 =
=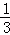 ;
;
當x從6,12,18,24這4個數中產生時,輸出的y值為3,故P3=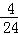 =
= ;
;
故輸出的y值為1的概率為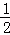 ,輸出的y值為2的概率為
,輸出的y值為2的概率為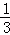 ,輸出的y值為3的概率為
,輸出的y值為3的概率為 ;
;
(II)當n=2100時,甲、乙所編程序各自輸出的y值為i(i=1,2,3)的頻率如下:
|
|
輸出y值為1的頻率 |
輸出y值為2的頻率 |
輸出y值為3的頻率 |
|
甲 |
|
|
|
|
乙 |
|
|
|
比較頻率趨勢與概率,可得乙同學所編程序符合算法要求的可能性較大;
(III)隨機變量ξ的可能取值為:0,1,2,3,P(ξ=0)=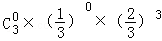 =
=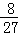 ,P(ξ=1)=
,P(ξ=1)= =
=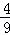
P(ξ=2)=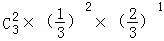 =
=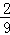 ,P(ξ=3)=
,P(ξ=3)=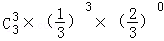 =
=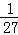 ,故ξ的分布列為:
,故ξ的分布列為:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
所以所求的數學期望Eξ=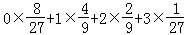 =1
=1


科目:高中數學 來源: 題型:
 已知某算法的程序框圖如圖所示,若將輸出的(x,y)值依次記為(x1,y1),(x2,y2),…(xn,yn),…
已知某算法的程序框圖如圖所示,若將輸出的(x,y)值依次記為(x1,y1),(x2,y2),…(xn,yn),…查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com