
【題目】已知圓![]() ,直線
,直線![]() 過定點
過定點![]()
(1)若直線![]() 與圓
與圓![]() 相切,求直線
相切,求直線![]() 的方程。
的方程。
(2)若直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程。
的方程。
【答案】(1)![]() (2)
(2)![]()
【解析】試題分析:(1)若直線![]() 的斜率不存在,則直線
的斜率不存在,則直線![]() ,符合題意;若直線
,符合題意;若直線![]() 的斜率存在,設直線
的斜率存在,設直線![]() 的方程為
的方程為![]() ,由題意知,圓心
,由題意知,圓心![]() 到已知直線
到已知直線![]() 的距離等于半徑
的距離等于半徑![]() ,由此利用點到直線的距離公式得
,由此利用點到直線的距離公式得![]() ,從而求出直線的方程;(2)設直線方程為
,從而求出直線的方程;(2)設直線方程為![]() ,由弦長
,由弦長![]() 求出弦心距
求出弦心距![]() ,由此利用點到直線距離公式求出
,由此利用點到直線距離公式求出![]() 或
或![]() ,從而能求出直線
,從而能求出直線![]() 的方程.
的方程.
試題解析:(1)圓![]() 的圓心
的圓心![]() ,半徑為2,
,半徑為2,
當直線![]() 的斜率不存在時,
的斜率不存在時,![]() 為
為![]() ,顯然滿足條件,
,顯然滿足條件,
當直線![]() 的斜率存在時,設
的斜率存在時,設![]() 的方程為
的方程為![]() 即
即![]()
圓心到![]() 的距離
的距離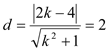 ,所以
,所以![]() ,
,![]() 的方程為
的方程為![]()
綜上得所求![]() 的方程為
的方程為![]() 或
或![]() .
.
(2)由題意得圓心到![]() 的距離為
的距離為![]()
由(1)知當直線![]() 的斜率不存在時,不滿足題意
的斜率不存在時,不滿足題意
當直線![]() 的斜率存在時,設
的斜率存在時,設![]() 的方程為
的方程為![]() 即
即![]()
圓心到![]() 的距離
的距離![]() ,所以
,所以![]() ,
,
![]() 的方程為
的方程為![]() 或
或![]()


科目:高中數學 來源: 題型:
【題目】某公司有30名男職員和20名女職員,公司進行了一次全員參與的職業能力測試,現隨機詢問了該公司5名男職員和5名女職員在測試中的成績(滿分為30分),可知這5名男職員的測試成績分別為16,24,18,
22,20,5名女職員的測試成績分別為18,23,23,18,23,則下列說法一定正確的是( )
A. 這種抽樣方法是分層抽樣
B. 這種抽樣方法是系統抽樣
C. 這5名男職員的測試成績的方差大于這5名女職員的測試成績的方差
D. 該測試中公司男職員的測試成績的平均數小于女職員的測試成績的平均數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示是某企業2010年至2016年污水凈化量(單位: 噸)的折線圖.
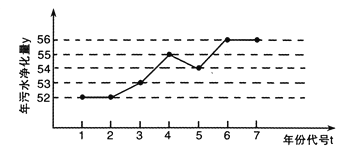
注: 年份代碼1-7分別對應年份2010-2016.
(1)由折線圖看出,可用線性回歸模型擬合![]() 和
和![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,預測
的回歸方程,預測![]() 年該企業污水凈化量;
年該企業污水凈化量;
(3)請用數據說明回歸方程預報的效果.
附注: 參考數據:![]() ;
;
參考公式:相關系數 ,回歸方程
,回歸方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分別為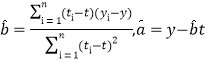 ;
;
反映回歸效果的公式為: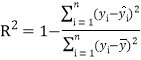 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回歸的效果越好.
,表示回歸的效果越好.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (其中
(其中![]() 為常數,
為常數,![]() ).(Ⅰ)求函數
).(Ⅰ)求函數![]() 的單調區間;(Ⅱ)當
的單調區間;(Ⅱ)當![]() 時,是否存在實數
時,是否存在實數![]() ,使得當
,使得當![]() 時,不等式
時,不等式![]() 恒成立?如果存在,求
恒成立?如果存在,求![]() 的取值范圍;如果不存在,請說明理由(其中
的取值范圍;如果不存在,請說明理由(其中![]() 是自然對數的底數,
是自然對數的底數,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .現提供
.現提供![]() 的大致圖像的8個選項:
的大致圖像的8個選項:
(A)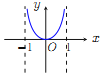 (B)
(B)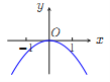 (C)
(C) (D)
(D)
(E) (F)
(F)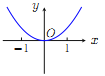 (G)
(G)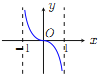 (H)
(H)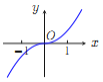
(Ⅰ)請你作出選擇,你選的是( );
(Ⅱ)對于函數圖像的判斷,往往只需了解函數的基本性質.為了驗證你的選擇的正確性,請你解決下列問題:
①![]() 的定義域是 ;
的定義域是 ;
②就奇偶性而言, ![]() 是 ;
是 ;
③當![]() 時,
時, ![]() 的符號為正還是負?并證明你的結論.
的符號為正還是負?并證明你的結論.
(解決了上述三個問題,你要調整你的選項,還來得及.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的圓臺中,AC是下底面圓O的直徑,EF是上底面圓O![]() 的直徑,FB是圓臺的一條母線.
的直徑,FB是圓臺的一條母線.
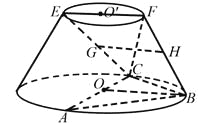
(Ⅰ)已知G,H分別為EC,FB的中點,求證:GH∥平面ABC;
(Ⅱ)已知EF=FB=![]() AC=
AC=![]() ,AB=BC.求二面角
,AB=BC.求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com