
【題目】如圖所示是某企業2010年至2016年污水凈化量(單位: 噸)的折線圖.
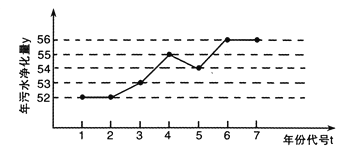
注: 年份代碼1-7分別對應年份2010-2016.
(1)由折線圖看出,可用線性回歸模型擬合![]() 和
和![]() 的關系,請用相關系數加以說明;
的關系,請用相關系數加以說明;
(2)建立![]() 關于
關于![]() 的回歸方程,預測
的回歸方程,預測![]() 年該企業污水凈化量;
年該企業污水凈化量;
(3)請用數據說明回歸方程預報的效果.
附注: 參考數據:![]() ;
;
參考公式:相關系數 ,回歸方程
,回歸方程![]() 中斜率和截距的最小;
中斜率和截距的最小;
二乘法估汁公式分別為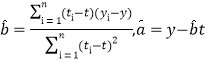 ;
;
反映回歸效果的公式為: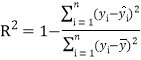 ,其中
,其中![]() 越接近于
越接近于![]() ,表示回歸的效果越好.
,表示回歸的效果越好.
【答案】(1) 見解析;(2) 預測![]() 年該企業污水凈化量約為
年該企業污水凈化量約為![]() 噸;(3) 回歸方程預測的效果是良好的.
噸;(3) 回歸方程預測的效果是良好的.
【解析】試題分析:(1)先求![]() ,再將折線圖中的數據代入參考公式可得相關系數,最后根據數值進行判斷相關性, (2) 將折線圖中的數據代入參考公式可得
,再將折線圖中的數據代入參考公式可得相關系數,最后根據數值進行判斷相關性, (2) 將折線圖中的數據代入參考公式可得![]() ,再根據線性回歸方程恒過
,再根據線性回歸方程恒過![]() ,解出
,解出![]() ,最后求
,最后求![]() 所對應函數值
所對應函數值![]() ,(3) 將折線圖中的數據代入參考公式可得
,(3) 將折線圖中的數據代入參考公式可得![]() ,再根據數據說明預測的效果.
,再根據數據說明預測的效果.
試題解析:(1) 由折線圖中的數據和附注中的參考數據得,
![]() ,所以
,所以![]() .因為
.因為![]() 與
與![]() 的相關系數近似為
的相關系數近似為![]() ,說明
,說明![]() 與
與![]() 的線性相關程度相當大,從而可以用線性回歸模型擬合
的線性相關程度相當大,從而可以用線性回歸模型擬合![]() 與
與![]() 的關系.
的關系.
(2) 由![]() 及(1)得
及(1)得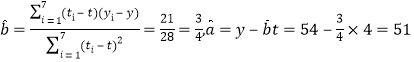 ,
,
所以![]() 關于
關于![]() 的回舊方程為:
的回舊方程為: ![]() , 將
, 將![]() 年對應的
年對應的![]() 代入得
代入得![]() ,
,
所以預測![]() 年該企業污水凈化量約為
年該企業污水凈化量約為![]() 噸.
噸.
(3) 因為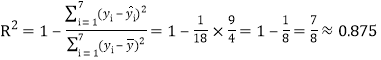 ,所以“污水凈化量的差異” 有
,所以“污水凈化量的差異” 有![]() 是由年份引起的,這說明回歸方程預測的效果是良好的.
是由年份引起的,這說明回歸方程預測的效果是良好的.


 優翼小幫手同步口算系列答案
優翼小幫手同步口算系列答案科目:高中數學 來源: 題型:
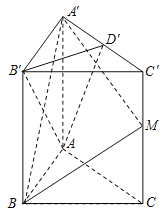
【題目】(本小題滿分15分)在直三棱柱![]() 中,底面
中,底面![]() 是邊長為2的正三角形,
是邊長為2的正三角形, ![]() 是棱
是棱![]() 的中點,且
的中點,且![]() .
.
(1)試在棱![]() 上確定一點
上確定一點![]() ,使
,使![]() 平面
平面![]() ;
;
(2)當點![]() 在棱
在棱![]() 中點時,求直線
中點時,求直線![]() 與平面
與平面![]() 所成角的大小的正弦值。
所成角的大小的正弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某科技興趣小組對晝夜溫差的大小與小麥新品種發芽多少之間的關系進行了研究,記錄了2016年12月1日至12月5日五天的晝夜溫差與相應每天100顆種子的發芽得到了如下數據:
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
溫差 | 9 | 11 | 10 | 12 | 13 |
發芽數 | 21 | 34 | 26 | 36 | 40 |
現從這5組數據中任選兩組,用余下的三組數據求回歸直線方程,再對被選取的兩組數據進行檢驗.
(Ⅰ)求選取的兩組數據恰好是不相鄰的兩天的概率;
(Ⅱ)若選取的是12月1日和12月5日的兩組數據,請根據余下的三組數據,求出![]() 與
與![]() 的線性回歸直線方程
的線性回歸直線方程![]() ;
;
(Ⅲ)若由線性回歸直線方程得到的估計值與所選出的兩組實際數據的誤差均不超過兩顆,則認為得到的回歸直線方程是可靠的,試判斷(Ⅱ)中得到的線性回歸直線方程是否可靠.
附:在線性回歸方程![]() 中,
中,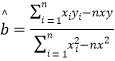 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某幾何體的三視圖如圖所示,P是正方形ABCD對角線的交點,G是PB的中點.
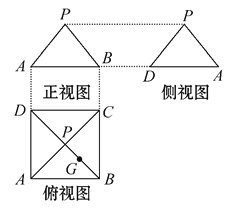
(1)根據三視圖,畫出該幾何體的直觀圖.
(2)在直觀圖中,①證明:PD∥平面AGC;
②證明:平面PBD⊥平面AGC.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)全集U={2,4,-(a-3)2},集合A={2,a2-a+2},若UA={-1},求實數a的值. (2)已知A={x|2a≤x≤a+3},B={x|x<-1或x>5},若A∩B=,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率為
,離心率為![]() ,直線
,直線![]() 與
與![]() 的兩個交點間的距離為
的兩個交點間的距離為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)分別過![]() 作
作![]() 滿足
滿足![]() ,設
,設![]() 與
與![]() 的上半部分分別交于
的上半部分分別交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com