
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
分析 根據p≠q,不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,只需該函數在($\frac{1}{2}$,1)內的導數大于0恒成立.
解答 解:由題意,要使不等式$\frac{f(p)-f(q)}{p-q}>0$恒成立,
只需f′(x)>0在($\frac{1}{2}$,1)上恒成立.
因為f′(x)=2x+a-$\frac{1}{{x}^{2}}$,所以2x+a-$\frac{1}{{x}^{2}}$>0在($\frac{1}{2}$,1)上恒成立,
即a>$\frac{1}{{x}^{2}}$-2x,x∈($\frac{1}{2}$,1)恒成立,
令g(x)=$\frac{1}{{x}^{2}}$-2x,x∈($\frac{1}{2}$,1),g′(x)=-$\frac{2}{{x}^{3}}$-2<0,
g(x)在($\frac{1}{2}$,1)遞減,g(x)<g($\frac{1}{2}$)=3
只需a≥3,
故選:D.
點評 本題考查了導數的幾何意義以及不等式恒成立問題的基本思路.屬于中檔題.


 53天天練系列答案
53天天練系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | ?n∈N,n2<2n | B. | ?n∈N,n2≥2n | C. | ?n∈N,n2≥2n | D. | ?n∈N,n2>2n |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 84 | B. | 78 | C. | 81 | D. | 96 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 增加了一項$\frac{1}{{2({k+1})}}$ | B. | 增加了兩項$\frac{1}{2k+1}$和$\frac{1}{{2({k+1})}}$ | ||
| C. | 增加了B中兩項,但又少了一項$\frac{1}{k+1}$ | D. | 增加了A中一項,但又少了一項$\frac{1}{k+1}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
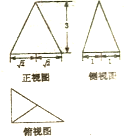
| A. | $2\sqrt{2}$ | B. | $2\sqrt{3}$ | C. | $6\sqrt{2}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com