
分析 (1)根據題意,可得$\frac{a-c}{c}$+$\frac{a-c}{a}$=3×$\frac{c}{a}$,變形可得a2=4c2,結合橢圓的標準方程可得a2=4以及c2=1,進而計算可得b2的值,將其代入橢圓的標準方程,計算可得答案;
(2)根據題意,設出直線l的斜率以及方程,聯立直線與橢圓的方程,解可得B的坐標,結合F、H的坐標可得向量$\overrightarrow{HF}$與$\overrightarrow{BF}$的坐標,分析可得BH為直徑的圓過點F,得$\overrightarrow{BF}$•$\overrightarrow{HF}$=0,進而有1×$\frac{9-4{k}^{2}}{4{k}^{2}+3}$-($\frac{4}{3}$)×$\frac{12k}{4{k}^{2}+3}$)=0,解可得k的值,即得答案.
解答 解:(1)根據題意,$\frac{|FA|}{|OF|}$+$\frac{|FA|}{|OA|}$=3e,有$\frac{a-c}{c}$+$\frac{a-c}{a}$=3×$\frac{c}{a}$,變形可得a2-c2=3c2,即a2=4c2,
又由a2=4,則c2=1,
b2=a2-c2=3,
故橢圓的方程為:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1;
(2)設直線l的斜率為k,(k≠0),則直線l的方程為y=k(x-2);
設B(xB,yB),
聯立方程$\left\{\begin{array}{l}{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\\{y=k(x-2)}\end{array}\right.$,消去y整理可得(4k2+3)x2-16k2x+16k2-12=0,
解可得x=2或x=$\frac{8{k}^{2}-6}{4{k}^{2}+3}$,
由題意可得xB=$\frac{8{k}^{2}-6}{4{k}^{2}+3}$,yB=$\frac{-12k}{4{k}^{2}+3}$,
由(1)可得:F(1,0),又由H(0,$\frac{4}{3}$),
則有$\overrightarrow{HF}$=(1,-$\frac{4}{3}$),$\overrightarrow{BF}$=($\frac{9-4{k}^{2}}{4{k}^{2}+3}$,$\frac{12k}{4{k}^{2}+3}$),
以BH為直徑的圓過點F,得$\overrightarrow{BF}$•$\overrightarrow{HF}$=0,
即1×$\frac{9-4{k}^{2}}{4{k}^{2}+3}$-($\frac{4}{3}$)×$\frac{12k}{4{k}^{2}+3}$)=0,
解可得k=-$\frac{9}{2}$或k=$\frac{1}{2}$.
點評 本題考查橢圓與直線的位置關系,涉及橢圓的簡單幾何性質以及標準方程的應用,關鍵是依據題意,求出橢圓的方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:選擇題
| A. | 若m∥α,α∩β=n,則 m∥n | B. | 若m∥α,m⊥n,則n⊥α | ||
| C. | 若m⊥α,n⊥α,則m∥n | D. | 若m?α,n?β,α⊥β,則m⊥n |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,每售出1噸該商品可獲利潤0.5萬元,未售出的商品,每1噸虧損0.3萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了130噸該商品.現以x(單位:噸,100≤x≤150)表示下一個銷售季度的市場需求量,T(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.
隨著經濟模式的改變,微商和電商已成為當今城鄉一種新型的購銷平臺.已知經銷某種商品的電商在任何一個銷售季度內,每售出1噸該商品可獲利潤0.5萬元,未售出的商品,每1噸虧損0.3萬元.根據往年的銷售經驗,得到一個銷售季度內市場需求量的頻率分布直方圖如右圖所示.已知電商為下一個銷售季度籌備了130噸該商品.現以x(單位:噸,100≤x≤150)表示下一個銷售季度的市場需求量,T(單位:萬元)表示該電商下一個銷售季度內經銷該商品獲得的利潤.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 事件A的概率P(A)必有0<P(A)<1 | |
| B. | 事件A的概率P(A)=0.999,則事件A是必然事件 | |
| C. | 用某種藥物對患有胃潰瘍的500名病人治療,結果有380人有明顯的療效,現有胃潰瘍的病人服用此藥,則估計其有明顯的療效的可能性為76% | |
| D. | 某獎券中獎率為50%,則某人購買此券10張,一定有5張中獎 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $\frac{1}{9}$ | B. | $\frac{5}{36}$ | C. | $\frac{3}{18}$ | D. | $\frac{1}{72}$ |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | [-1,0] | B. | [-1,+∞) | C. | [0,3] | D. | [3,+∞) |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1 | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
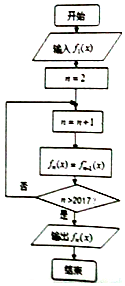 執行如圖的程序框圖,當n≥2,n∈Z時,fn(x)表示fn-1(x)的導函數,若輸入函數f1(x)=sinx-cosx,則輸出的函數fn(x)可化為( )
執行如圖的程序框圖,當n≥2,n∈Z時,fn(x)表示fn-1(x)的導函數,若輸入函數f1(x)=sinx-cosx,則輸出的函數fn(x)可化為( )| A. | $\sqrt{2}$sin(x+$\frac{π}{4}$) | B. | $\sqrt{2}$sin(x-$\frac{π}{4}$) | C. | -$\sqrt{2}$sin(x+$\frac{π}{4}$) | D. | -$\sqrt{2}$sin(x-$\frac{π}{4}$) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com