【題目】求直線l：ax－y＋b＝0經過兩直線l1：2x－2y－3＝0和l2：3x－5y＋1＝0交點的充要條件．
【答案】17a＋4b＝11.
【解析】試題分析：聯立兩條直線方程，可解得直線的交點坐標為
，將點
代入直線方程
，即可證明充分性，若
可得
將其帶入直線方程
，可得直線
恒過定點
，即可證明必要性.
試題解析：由
得交點P(
，
)．
若直線l：ax－y＋b＝0經過點P，
則a×－＋b＝0.∴17a＋4b＝11.
設a，b滿足17a＋4b＝11，則b＝
，
代入方程ax－y＋b＝0，得ax－y＋＝0，
整理，得
－a
＝0.
∴直線l：ax－y＋b＝0恒過點
，此點即為l1與l2的交點．
綜上，直線l：ax－y＋b＝0經過兩直線l1：2x－2y－3＝0和l2：3x－5y＋1＝0交點的充要條件為17a＋4b＝11.
同步練習強化拓展系列答案科目：高中數學 來源： 題型：
【題目】袋中裝有黑球和白球共7個，從中任取2個球都是白球的概率為
，現有甲，乙二人從袋中輪流摸取1球，甲先取，乙后取，然后甲再取，……，取后不放回，直到兩人中有一人取到白球即終止，每個球在每一次被取出的機會是等可能的.
（Ⅰ）求袋中原有白球的個數：
（Ⅱ）求取球次數
的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設函數
.
（1）函數
在區間
是單調函數，求實數
的取值范圍；
（2）若存在
，使得
成立，求滿足條件的最大整數
；
（3）如果對任意的
都有
成立，求實數的范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】8人排成一排照相，分別求下列條件下的不同照相方式的種數.
（1）其中甲、乙相鄰，丙、丁相鄰；
（2）其中甲、乙不相鄰，丙、丁不相鄰；
（要求寫出解答過程，并用數字作答）
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】學校藝術節對同一類的
，
，
，
四項參賽作品，只評一項一等獎，在評獎揭曉前，甲、乙、丙、丁四位同學對這四項參賽作品預測如下：
甲說：“是或作品獲得一等獎”；
乙說：“作品獲得一等獎”；
丙說：“，兩項作品未獲得一等獎”；
丁說：“是作品獲得一等獎”.
若這四位同學中只有兩位說的話是對的，則獲得一等獎的作品是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）△ABC中，角A，B，C所對的邊分別為a，b，c．已知a＝3，cos A＝
，B＝A＋
．
（1）求b的值；
（2）求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空間四邊形PABC的各邊及對角線長度都相等，D、E、F、G分別是AB、BC、CA、AP的中點，下列四個結論中成立的是
①BC∥平面PDF
②DF⊥平面PAE
③平面GDF∥平面PBC
④平面PAE⊥平面ABC．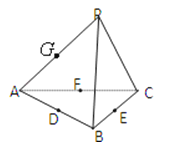
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知兩定點
， 
和一動點
，給出下列結論：
①若
，則點
的軌跡是橢圓；
②若
，則點
的軌跡是雙曲線；
③若
，則點
的軌跡是圓；
④若
，則點
的軌跡關于原點對稱；
⑤若直線
與
斜率之積等于
，則點
的軌跡是橢圓（除長軸兩端點）．
其中正確的是__________（填序號）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在極坐標系下，已知圓O：ρ=cosθ+sinθ和直線l：ρsin（θ﹣ 
）= 
．
（1）求圓O和直線l的直角坐標方程；
（2）當θ∈（0，π）時，求直線l與圓O公共點的極坐標．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com