
【題目】某超市從現有甲、乙兩種酸奶的日銷售量(單位:箱)的1200個數據(數據均在區間(0,50]內)中,按照5%的比例進行分層抽樣,統計結果按(0,10],(10,20],(20,30],(30,40],(40,50]分組,整理如下圖: 
(Ⅰ)寫出頻率分布直方圖(圖乙)中a的值;記所抽取樣本中甲種酸奶與乙種酸奶日銷售量的方差分別為 ![]() ,
, ![]() ,試比較
,試比較 ![]() 與
與 ![]() 的大小(只需寫出結論);
的大小(只需寫出結論);
(Ⅱ)從甲種酸奶日銷售量在區間(0,20]的數據樣本中抽取3個,記在(0,10]內的數據個數為X,求X的分布列;
(Ⅲ)估計1200個日銷售量數據中,數據在區間(0,10]中的個數.
【答案】解:(Ⅰ)由圖(乙)知,10(a+0.02+0.03+0.025+0.015)=1,
解得a=0.01,
根據圖甲的頻率分布比圖乙分散些,它的方差較大,
∴ ![]() ;
;
(Ⅱ)X的所有可能取值1,2,3;
則 ![]() ,
, ![]() ,
,![]() ,
,
其分布列如下:
X | 1 | 2 | 3 |
P |
|
|
|
(Ⅲ)由圖(甲)知,甲種酸奶的數據共抽取2+3+4+5+6=20個,
其中有4個數據在區間(0,10]內,
又因為分層抽樣共抽取了1200×5%=60個數據,
乙種酸奶的數據共抽取60﹣20=40個,
由(Ⅰ)知,乙種酸奶的日銷售量數據在區間(0,10]內的頻率為0.1,
故乙種酸奶的日銷售量數據在區間(0,10]內有40×0.1=4個.
故抽取的60個數據,共有4+4=8個數據在區間(0,10]內.
所以,在1200個數據中,在區間(0,10]內的數據有160個
【解析】(Ⅰ)由頻率和為1,列方程求出a的值,根據圖甲的頻率分布比圖乙分散些,它的方差較大,得出 ![]() ;(Ⅱ)根據X的所有可能取值,計算對應的概率,寫出分布列;(Ⅲ)由甲種和乙種酸奶的日銷售量數據在區間(0,10]內的頻率和頻數,
;(Ⅱ)根據X的所有可能取值,計算對應的概率,寫出分布列;(Ⅲ)由甲種和乙種酸奶的日銷售量數據在區間(0,10]內的頻率和頻數,
計算在1200個數據中應抽取的數據個數.
【考點精析】本題主要考查了頻率分布直方圖和離散型隨機變量及其分布列的相關知識點,需要掌握頻率分布表和頻率分布直方圖,是對相同數據的兩種不同表達方式.用緊湊的表格改變數據的排列方式和構成形式,可展示數據的分布情況.通過作圖既可以從數據中提取信息,又可以利用圖形傳遞信息;在射擊、產品檢驗等例子中,對于隨機變量X可能取的值,我們可以按一定次序一一列出,這樣的隨機變量叫做離散型隨機變量.離散型隨機變量的分布列:一般的,設離散型隨機變量X可能取的值為x1,x2,.....,xi,......,xn,X取每一個值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,則稱表為離散型隨機變量X 的概率分布,簡稱分布列才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】已知函數f(x)=sinx+λcosx的圖像的一個對稱中心是點( ![]() ,0),則函數g(x)=λsinxcosx+sin2x的圖像的一條對稱軸是直線( )
,0),則函數g(x)=λsinxcosx+sin2x的圖像的一條對稱軸是直線( )
A.x= ![]()
B.x= ![]()
C.x= ![]()
D.x=﹣ ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生寒假期間學習情況,學校對某班男、女學生學習時間進行調查,學習時間按整小時統計,調查結果繪成折線圖如下: 
(Ⅰ)已知該校有400名學生,試估計全校學生中,每天學習不足4小時的人數;
(Ⅱ)若從學習時間不少于4小時的學生中選取4人,設選到的男生人數為X,求隨機變量X的分布列;
(Ⅲ)試比較男生學習時間的方差 ![]() 與女生學習時間方差
與女生學習時間方差 ![]() 的大小.(只需寫出結論)
的大小.(只需寫出結論)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國南宋著名數學家秦九韶發現了從三角形三邊求三角形面積的“三斜公式”,設△ABC三個內角A、B、C所對的邊分別為a、b、c,面積為S,則“三斜求積”公式為 ![]() .若a2sinC=4sinA,(a+c)2=12+b2 , 則用“三斜求積”公式求得△ABC的面積為( )
.若a2sinC=4sinA,(a+c)2=12+b2 , 則用“三斜求積”公式求得△ABC的面積為( )
A.![]()
B.2
C.3
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]已知曲線C的極坐標方程是ρ=2cosθ,以極點為平面直角坐標系的原點,極軸為x軸的正半軸,建立平面直角坐標系,直線L的參數方程是 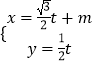 (t為參數).
(t為參數).
(1)求曲線C的直角坐標方程和直線L的普通方程;
(2)設點P(m,0),若直線L與曲線C交于A,B兩點,且|PA||PB|=1,求實數m的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對函數f(x),如果存在x0≠0使得f(x0)=﹣f(﹣x0),則稱(x0 , f(x0))與(﹣x0 , f(﹣x0))為函數圖象的一組奇對稱點.若f(x)=ex﹣a(e為自然數的底數)存在奇對稱點,則實數a的取值范圍是( )
A.(﹣∞,1)
B.(1,+∞)
C.(e,+∞)
D.[1,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,拋物線E:y2=2px(p>0)與圓O:x2+y2=8相交于A,B兩點,且點A的橫坐標為2.過劣弧AB上動點P(x0 , y0)作圓O的切線交拋物線E于C,D兩點,分別以C,D為切點作拋物線E的切線l1 , l2 , l1與l2相交于點M.
(Ⅰ)求p的值;
(Ⅱ)求動點M的軌跡方程.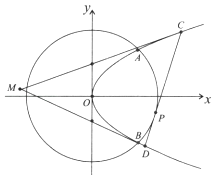
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓內接△ABC中,D為BC上一點,且△ADC為正三角形,點E為BC的延長線上一點,AE為圓O的切線. 
(1)求∠BAE 的度數;
(2)求證: ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(2015·湖南)某工作的三視圖如圖3所示,現將該工作通過切削,加工成一個體積盡可能大的正方體新工件,并使新工件的一個面落在原工作的一個面內,則原工件材料的利用率為(材料利用率=新工件的體積/原工件的體積)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com