
【題目】如圖,已知直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的中點,
的中點,![]() 是
是![]() 上一點,且
上一點,且![]() .
.
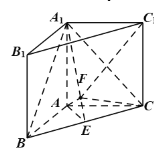
(Ⅰ)證明:![]() 平面
平面![]() ;
;
(Ⅱ)求三棱錐![]() 的體積.
的體積.
 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】某企業有甲、乙兩套設備生產同一種產品,為了檢測兩套設備的生產質量情況,隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本,檢測一項質量指標值,若該項質量指標值落在![]() 內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖1是乙套設備的樣本的頻率分布直方圖.
內,則為合格品,否則為不合格品.表1是甲套設備的樣本的頻數分布表,圖1是乙套設備的樣本的頻率分布直方圖.
表1:甲套設備的樣本的頻數分布表
質量指標值 |
|
|
|
|
|
|
頻數 | 1 | 5 | 18 | 19 | 6 | 1 |
圖1:乙套設備的樣本的頻率分布直方圖
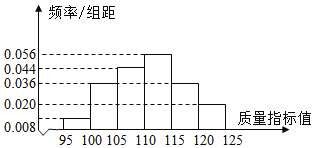
(1)根據表1和圖1,通過計算合格率對兩套設備的優劣進行比較;
(2)填寫下面列聯表,并根據列聯表判斷是否有![]() 的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關.
甲套設備 | 乙套設備 | 合計 | |
合格品 | |||
不合格品 | |||
合計 |
附:
| 0.15 | 0.10 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
參考公式: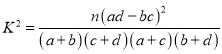 ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() 為自然對數的底數).
為自然對數的底數).
(1)若曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直,求
垂直,求![]() 的單調區間;
的單調區間;
(2)若函數![]() 有兩個極值點,求實數
有兩個極值點,求實數![]() 的取值范圍;
的取值范圍;
(3)證明:當![]() 時,
時,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐A-BCDE,其中AC=BC=2,AC⊥BC,CD//BE且CD=2BE,CD⊥平面ABC,F為AD的中點.
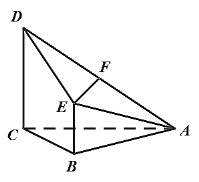
(1)求證:EF//平面ABC;
(2)設M是AB的中點,若DM與平面ABC所成角的正切值為![]() ,求平面ACD與平面ADE夾角的余弦值.
,求平面ACD與平面ADE夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設直線l的方程為(a﹣1)x+y+a+3=0,(a∈R).
(1)若直線l在兩坐標軸上截距的絕對值相等,求直線l的方程;
(2)若直線l不經過第一象限,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知橢圓![]()
![]() (
(![]() )的半焦距為
)的半焦距為![]() ,原點
,原點![]() 到經過兩點
到經過兩點![]() ,
,![]() 的直線的距離為
的直線的距離為![]() .
.
(Ⅰ)求橢圓![]() 的離心率;
的離心率;
(Ⅱ)如圖,![]() 是圓
是圓![]()
![]() 的一條直徑,若橢圓
的一條直徑,若橢圓![]() 經過
經過![]() ,
,![]() 兩點,求橢圓
兩點,求橢圓![]() 的方程.
的方程.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知兩點A(0,﹣1),B(0,1),直線PA,PB相交于點P,且它們的斜率之積是![]() ,記點P軌跡為C.
,記點P軌跡為C.
(1)求曲線C的軌跡方程;
(2)直線l與曲線C交于M,N兩點,若|AM|=|AN|,求直線l的斜率k的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com