Question

2．某城市有一直角梯形綠地ABCD，其中∠ABC=∠BAD=90°，AD=DC=2km，BC=1km．現過邊界CD上的點E處鋪設一條直的灌溉水管EF，將綠地分成面積相等的兩部分．

（1）如圖①，若E為CD的中點，F在邊界AB上，求灌溉水管EF的長度；
（2）如圖②，若F在邊界AD上，求灌溉水管EF的最短長度．

Answer 1

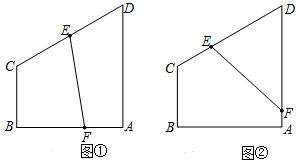
分析 （1）取AB中點G，則四邊形BCEF的面積為$\frac{1}{2}{S_{梯形ABCD}}={S_{梯形BCEG}}+{S_{△EFG}}$，求出GF，即可求灌溉水管EF的長度；
（2）△ADC中，由余弦定理，得$EF=\sqrt{{a^2}+{b^2}-ab}≥\sqrt{ab}=\sqrt{3}$，即可求灌溉水管EF的最短長度．

解答 解：（1）因為AD=DC=2，BC=1，∠ABC=∠BAD=90°，
所以$AB=\sqrt{3}$，…（2分）
取AB中點G，則四邊形BCEF的面積為$\frac{1}{2}{S_{梯形ABCD}}={S_{梯形BCEG}}+{S_{△EFG}}$，
即$\frac{1}{2}×\frac{1}{2}×\sqrt{3}（1+2）$=$\frac{1}{2}×\frac{{\sqrt{3}}}{2}（1+\frac{3}{2}）+\frac{1}{2}GF×\frac{3}{2}$，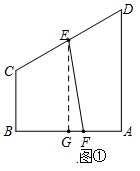

解得$GF=\frac{{\sqrt{3}}}{6}$，…（6分）
所以$EF=\sqrt{{{（\frac{3}{2}）}^2}+{{（\frac{{\sqrt{3}}}{6}）}^2}}=\frac{{\sqrt{21}}}{3}$（km）．
故灌溉水管EF的長度為$\frac{{\sqrt{21}}}{3}$km．…（8分）
（2）設DE=a，DF=b，在△ABC中，$CA=\sqrt{{1^2}+{{（\sqrt{3}）}^2}}=2$，
所以在△ADC中，AD=DC=CA=2，
所以∠ADC=60°，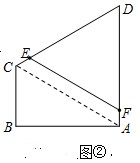
所以△DEF的面積為${S_{△DEF}}=\frac{1}{2}absin60°=\frac{{\sqrt{3}}}{4}ab$，
又${S_{梯形ABCD}}=\frac{{3\sqrt{3}}}{2}$，所以$\frac{{\sqrt{3}}}{4}ab=\frac{{3\sqrt{3}}}{4}$，即ab=3．…（12分）
在△ADC中，由余弦定理，得$EF=\sqrt{{a^2}+{b^2}-ab}≥\sqrt{ab}=\sqrt{3}$，
當且僅當$a=b=\sqrt{3}$時，取“=”．
故灌溉水管EF的最短長度為$\sqrt{3}$km．…（16分）

點評 本題考查利用數學知識解決實際問題，考查基本不等式的運用，考查余弦定理，屬于中檔題．