
【題目】設常數![]() ,函數
,函數![]()
(1)當![]() 時,判斷
時,判斷![]() 在
在![]() 上單調性,并加以證明;
上單調性,并加以證明;
(2)當![]() 時,研究
時,研究![]() 的奇偶性,并說明理由;
的奇偶性,并說明理由;
(3)當![]() 時,若存在區間
時,若存在區間![]() 使得
使得![]() 在
在![]() 上的值域為
上的值域為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() 在
在![]() 上是單調遞增.證明見解析(2)見解析;(3)
上是單調遞增.證明見解析(2)見解析;(3)![]()
【解析】
(1)由函數的單調性定義即可證明。
(2)由函數的奇偶性定義即可證明。
(3)首先證明函數的單調性,當![]() 時證明函數
時證明函數![]() 在
在![]() 上單調遞增,即
上單調遞增,即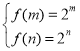 ,解關于
,解關于![]() 一元二次方程即可;
一元二次方程即可;
同理當![]() 時,求出
時,求出![]() 單調區間,當函數是單調遞減時,則
單調區間,當函數是單調遞減時,則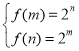 代入化簡即可求解。
代入化簡即可求解。
解:(1)當![]() 時,
時,![]()
任取![]()
則![]()
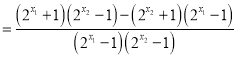
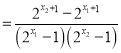
∵![]()
∴![]()
∴![]()
∴![]()
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
即:![]()
∴![]() 在
在![]() 上是單調遞增.
上是單調遞增.
(2)①當![]() 時,
時,![]()
∵![]()
∴![]() 為偶函數
為偶函數
②當![]() 時,
時,![]()
![]() ,則
,則![]()
![]() 當
當![]() 且
且![]() 時,
時,![]() 的定義域為
的定義域為![]()
定義域不關于原點對稱
∴![]() 為非奇非偶函數
為非奇非偶函數
![]() 當
當![]() 時,
時,![]() ,
,![]() 的定義域為
的定義域為![]()
定義域關于原點對稱
![]()
∴![]() 為奇函數.
為奇函數.
(3)①當![]() 時,
時,![]() 定義域為
定義域為![]()
![]()
∵![]() 單調遞增,∴
單調遞增,∴![]() 單調遞減
單調遞減
∴![]() 在
在![]() 上單調遞增
上單調遞增
由題意得: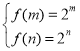
∴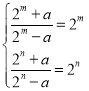
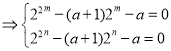
∴![]() ,
,![]() 是一元二次方程:
是一元二次方程:
![]() 的兩個不等的正根
的兩個不等的正根
∴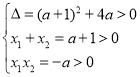
![]()
②當![]() 時,
時,![]() 定義域為
定義域為![]()
∵當![]() 時,
時,![]() 的值域為
的值域為![]()
∴![]() ,
,![]()
當![]() 時,
時,![]()
∵![]() 單調遞增,∴
單調遞增,∴![]() 單調遞減
單調遞減
∴![]() 在
在![]() 上單調遞減
上單調遞減
∴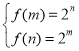
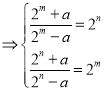
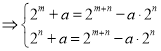
∴![]()
∵![]()
∴![]()
∴![]()
綜上所述:![]() 的取值范圍是
的取值范圍是![]() .
.


 優百分課時互動系列答案
優百分課時互動系列答案 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案科目:高中數學 來源: 題型:
【題目】甲、乙兩名槍手進行射擊比賽,每人各射擊三次,甲三次射擊命中率均為![]() ;乙第一次射擊的命中率為
;乙第一次射擊的命中率為![]() ,若第一次未射中,則乙進行第二次射擊,射擊的命中率為
,若第一次未射中,則乙進行第二次射擊,射擊的命中率為![]() ,如果又未中,則乙進行第三次射擊,射擊的命中率為
,如果又未中,則乙進行第三次射擊,射擊的命中率為![]() .乙若射中,則不再繼續射擊.則甲三次射擊命中次數的期望為_____,乙射中的概率為_____.
.乙若射中,則不再繼續射擊.則甲三次射擊命中次數的期望為_____,乙射中的概率為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】眾所周知,大型網絡游戲(下面簡稱網游)的運行必須依托于網絡的基礎上,否則會出現頻繁掉線的情況,進而影響游戲的銷售和推廣,某網游經銷在甲地區5個位置對兩種類型的網絡(包括“電信”和“網通”)在相同條件下進行游戲掉線的測試,得到數據如下:
位置 類型 | A | B | C | D | E |
電信 | 4 | 3 | 8 | 6 | 12 |
網通 | 5 | 7 | 9 | 4 | 3 |
(1)如果在測試中掉線次數超過5次,則網絡狀況為“糟糕”,否則為“良好”,那么在犯錯誤的概率不超過0.15的前提下,能否說明網絡狀況與網絡的類型有關?
(2)若該游戲經銷商要在上述接受測試的電信的5個地區中任選2個作為游戲推廣,求A,B兩地區至少選到一個的概率.
參考公式: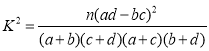 .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 的兩個頂點
的兩個頂點![]() 的坐標分別為
的坐標分別為![]() ,
,![]() ,且
,且![]() 所在直線的斜率之積等于
所在直線的斜率之積等于![]() ,記頂點
,記頂點![]() 的軌跡為
的軌跡為![]() .
.
(Ⅰ)求頂點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,點
兩點,點![]() 在曲線
在曲線![]() 上,且
上,且![]() 為
為![]() 的重心(
的重心(![]() 為坐標原點),求證:
為坐標原點),求證:![]() 的面積為定值,并求出該定值.
的面積為定值,并求出該定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() 為參數),在以坐標原點
為參數),在以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸的極坐標系中,點
軸的正半軸為極軸的極坐標系中,點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的直角坐標方程與曲線
的直角坐標方程與曲線![]() 的普通方程;
的普通方程;
(2)若![]() 是曲線
是曲線![]() 上的動點,
上的動點,![]() 為線段
為線段![]() 的中點,求點
的中點,求點![]() 到直線
到直線![]() 的距離的最大值.
的距離的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com