
【題目】某市場研究人員為了了解產業園引進的甲公司前期的經營狀況,對該公司2019年連續六個月的利潤進行了統計,并根據得到的數據繪制了相應的折線圖,如圖所示:
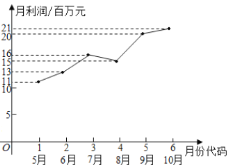
(1)由折線圖可以看出,可用線性回歸模型擬合月利潤![]() (單位:百萬元)與月份代碼
(單位:百萬元)與月份代碼![]() 之間的關系,求
之間的關系,求![]() 關于
關于![]() 的線性回歸方程,并預測該公司2020年4月份的利潤;
的線性回歸方程,并預測該公司2020年4月份的利潤;
(2)甲公司新研制了一款產品,需要采購一批新型材料,現有A,B兩種型號的新型材料可供選擇,按規定每種新型材料最多可使用4個月,但新材料的不穩定性會導致材料的使用壽命不同,現對A,B兩種型號的新型材料對應的產品各100件進行科學模擬測試,得到兩種新型材料使用壽命的頻數統計如下表:

經甲公司測算平均每件新型材料每月可以帶來6萬元收人入,不考慮除采購成本之外的其他成本,A型號材料每件的采購成本為10萬元,B型號材料每件的采購成本為12萬元.假設每件新型材料的使用壽命都是整月數,且以頻率作為每件新型材料使用壽命的概率,如果你是甲公司的負責人,以每件新型材料產生利潤的平均值為決策依據,你會選擇采購哪款新型材料?
參考數據:![]() ,
,![]() .
.
參考公式:回歸直線方程![]() ,其中
,其中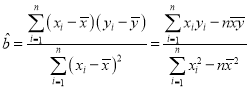 .
.
【答案】(1)線性回歸方程為![]() ,利潤為33百萬元;(2)應該采購A型新材料.
,利潤為33百萬元;(2)應該采購A型新材料.
【解析】
(1)根據題設的折線圖中的統計數據,求得其平均數,以及回歸系數![]() 和
和![]() ,求得回歸直線的方程,代入
,求得回歸直線的方程,代入![]() 時,即可作出預測;
時,即可作出預測;
(2)由頻率估計概率,求得每件A,B型新材料可產生的利潤的平均值,即可得到結論.
(1)由題意,根據題設的折線圖可知,統計數據![]() 共有6組,
共有6組,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
計算可得![]() ,
,![]() ,
,
所以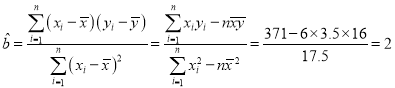 ,
,
![]() ,
,
所以月度利潤![]() 與月份代碼
與月份代碼![]() 之間的線性回歸方程為
之間的線性回歸方程為![]() .
.
當![]() 時,可得
時,可得![]() .
.
故預計甲公司2020年4月份的利潤為33百萬元.
(2)由頻率估計概率,每件A型新材料可使用1個月,2個月,3個月和4個月的概率,
分別為0.2,0.35,0.35和0.1,
所以每件A型新材料可產生的利潤的平均值為
![]() (萬元).
(萬元).
由頻率估計概率,每件B型新材料可使用1個月,2個月,3個月和4個月的概率,
分別為0.15,0.2,0.4和0.25,
所以每件B型新材料可產生的利潤的平均值為
![]() (萬元).
(萬元).
因為![]() ,所以應該采購A型新材料.
,所以應該采購A型新材料.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:高中數學 來源: 題型:
【題目】某人經營淡水池塘養草魚,根據過去![]() 期的養殖檔案,該池塘的養殖重量
期的養殖檔案,該池塘的養殖重量![]() (百斤)都在
(百斤)都在![]() 百斤以上,其中不足
百斤以上,其中不足![]() 百斤的有
百斤的有![]() 期,不低于
期,不低于![]() 百斤且不超過
百斤且不超過![]() 百斤的有
百斤的有![]() 期,超過
期,超過![]() 百斤的有
百斤的有![]() 期.根據統計,該池塘的草魚重量的增加量
期.根據統計,該池塘的草魚重量的增加量![]() (百斤)與使用某種餌料的質量
(百斤)與使用某種餌料的質量![]() (百斤)之間的關系如圖所示.
(百斤)之間的關系如圖所示.
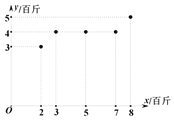
(1)根據數據可知![]() 與
與![]() 具有線性相關關系,請建立
具有線性相關關系,請建立![]() 關于
關于![]() 的回歸方程
的回歸方程![]() ;如果此人設想使用某種餌料
;如果此人設想使用某種餌料![]() 百斤時,草魚重量的增加量須多于
百斤時,草魚重量的增加量須多于![]() 百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
百斤,請根據回歸方程計算,確定此方案是否可行?并說明理由.
(2)養魚的池塘對水質含氧量與新鮮度要求較高,某商家為該養殖戶提供收費服務,即提供不超過![]() 臺增氧沖水機,每期養殖使用的沖水機運行臺數與魚塘的魚重量
臺增氧沖水機,每期養殖使用的沖水機運行臺數與魚塘的魚重量![]() 有如下關系:
有如下關系:
魚的重量(單位:百斤) |
|
|
|
沖水機只需運行臺數 |
|
|
|
若某臺增氧沖水機運行,則商家每期可獲利![]() 千元;若某臺沖水機未運行,則商家每期虧損
千元;若某臺沖水機未運行,則商家每期虧損![]() 千元.視頻率為概率,商家欲使每期沖水機總利潤的均值達到最大,應提供幾臺增氧沖水機?
千元.視頻率為概率,商家欲使每期沖水機總利潤的均值達到最大,應提供幾臺增氧沖水機?
附:對于一組數據![]() ,其回歸方程
,其回歸方程![]() 的斜率和截距的最小二乘估計公式分別為
的斜率和截距的最小二乘估計公式分別為
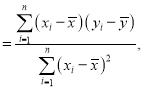
![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=lnx﹣sinx,記f(x)的導函數為f'(x).
(1)若h(x)=ax![]() f'(x)是(0,+∞)上的單調遞增函數,求實數a的取值范圍;
f'(x)是(0,+∞)上的單調遞增函數,求實數a的取值范圍;
(2)若x∈(0,2π),試判斷函數f(x)的極值點個數,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,AB是平面![]() 的斜線段,A為斜足,點C滿足
的斜線段,A為斜足,點C滿足![]() ,且在平面
,且在平面![]() 內運動,則有以下幾個命題:
內運動,則有以下幾個命題:

①當![]() 時,點C的軌跡是拋物線;
時,點C的軌跡是拋物線;
②當![]() 時,點C的軌跡是一條直線;
時,點C的軌跡是一條直線;
③當![]() 時,點C的軌跡是圓;
時,點C的軌跡是圓;
④當![]() 時,點C的軌跡是橢圓;
時,點C的軌跡是橢圓;
⑤當![]() 時,點C的軌跡是雙曲線.
時,點C的軌跡是雙曲線.
其中正確的命題是__________.(將所有正確的命題序號填到橫線上)
查看答案和解析>>
科目:高中數學 來源: 題型:
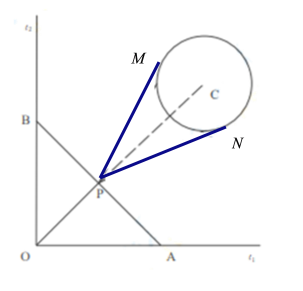
【題目】如圖,在一旅游區內原有兩條互相垂直且相交于點O的道路l1,l2,一自然景觀的邊界近似為圓形,其半徑約為1千米,景觀的中心C到l1,l2的距離相等,點C到點O的距離約為10千米.現擬新建四條游覽道路方便游客參觀,具體方案:在線段OC上取一點P,新建一條道路OP,并過點P新建兩條與圓C相切的道路PM,PN(M,N為切點),同時過點P新建一條與OP垂直的道路AB(A,B分別在l1,l2上).為促進沿途旅游經濟,新建道路長度之和越大越好,求新建道路長度之和的最大值.(所有道路寬度忽略不計)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題12分)
A、B是治療同一種疾病的兩種藥,用若干試驗組進行對比試驗。每個試驗組由4只小白鼠組成,其中2只服用A,另2只服用B,然后觀察療效。若在一個試驗組中,服用A有效的小白鼠的只數比服用B有效的多,就稱該試驗組為甲類組。設每只小白鼠服用A有效的概率為![]() ,服用B有效的概率為
,服用B有效的概率為![]() 。
。
(Ⅰ)求一個試驗組為甲類組的概率;
(Ⅱ) 觀察3個試驗組,用![]() 表示這3個試驗組中甲類組的個數,求
表示這3個試驗組中甲類組的個數,求![]() 的分布列和數學期望。
的分布列和數學期望。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com