
科目: 來源: 題型:
【題目】在平面直角坐標系xOy中,拋物線y=ax2+4x+c(a≠0)經過點A(3,﹣4)和B(0,2).
(1)求拋物線的表達式和頂點坐標;
(2)將拋物線在A、B之間的部分記為圖象M(含A、B兩點).將圖象M沿直線x=3翻折,得到圖象N.若過點C(9,4)的直線y=kx+b與圖象M、圖象N都相交,且只有兩個交點,求b的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖是拋物線型拱橋,當拱頂離水面![]() 時,水面寬
時,水面寬![]() 為
為![]() .當水面上升
.當水面上升![]() 時達到警戒水位,此時拱橋內的水面寬度是多少
時達到警戒水位,此時拱橋內的水面寬度是多少![]() ?
?
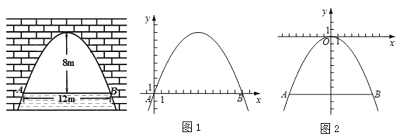
下面給出了解決這個問題的兩種方法,請補充完整:
方法一:如圖1.以點![]() 為原點,
為原點,![]() 所在直線為
所在直線為![]() 軸,建立平面直角坐標系
軸,建立平面直角坐標系![]() ,此時點
,此時點![]() 的坐標為_______,拋物線的項點坐標為_______,可求這條拋物線所表示的二次函數解析式為_______.當
的坐標為_______,拋物線的項點坐標為_______,可求這條拋物線所表示的二次函數解析式為_______.當![]() 時,求出此時自變量
時,求出此時自變量![]() 的取值,即可解決這個問題.
的取值,即可解決這個問題.
方法二:如圖2,以拋物線頂點為原點,對稱軸為![]() 軸.建立平面直角坐標系
軸.建立平面直角坐標系![]() ,這時這條拋物線所表示的二次函數的解析式為_______,當水面達到警戒水位,即
,這時這條拋物線所表示的二次函數的解析式為_______,當水面達到警戒水位,即![]() _______時,求出此時自變量
_______時,求出此時自變量![]() 的取值為_______,從而得水面寬為
的取值為_______,從而得水面寬為![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】己知二次函數![]() .
.
(1)將![]() 化成
化成![]() 的形式為________;
的形式為________;
(2)此函數與![]() 軸的交點坐標為________;
軸的交點坐標為________;
(3)在平面直角坐標系![]() 中畫出這個二次函數的圖象(不用列表);
中畫出這個二次函數的圖象(不用列表);
(4)直接寫出當![]() 時,
時,![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目: 來源: 題型:
【題目】數學課上,老師提出了這樣一個問題:如圖,己知![]() .求作:過
.求作:過![]() 三點的圓.
三點的圓.
小蕓是這樣思考的:圓心確定一個圈的位置,半徑確定一個圓的大小要作同時經過幾個定點的圓,就是要先找到一個點,使得這個點到這幾個定點的距離都相等.這樣既定了圓心,又定了半徑,就能畫出滿足條件的圓了.
小智聽了小蕓的分析后,按照這個思路很快就畫出了一個過![]() 三點的圓.
三點的圓.
請你在答題紙上而出這個圓,并寫出作圖的主要依據,

查看答案和解析>>
科目: 來源: 題型:
【題目】已知二次函數![]() ,
,![]() 與
與![]() 的部分對應值如下表所示:
的部分對應值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四個論斷:
①拋物線![]() 的頂點為
的頂點為![]() ;
;
②![]() ;
;
③關于![]() 的方程
的方程![]() 的解為
的解為![]() ;
;
④![]() .
.
其中,正確的有___________________
查看答案和解析>>
科目: 來源: 題型:
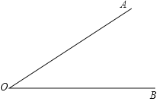
【題目】下面是小華設計的“作一個角等于已知角的2倍”的尺規作圖過程.
已知:![]() .
.
求作:![]() ,使得
,使得![]() .
.
作法:如圖,
①在射線![]() 上任取一點
上任取一點![]() ;
;
②作線段![]() 的垂直平分線,交
的垂直平分線,交![]() 于點
于點![]() ,交
,交![]() 于點
于點![]() ;
;
③連接![]() ;
;
所以![]() 即為所求作的角.
即為所求作的角.
根據小華設計的尺規作圖過程,
(1)使用直尺和圓規補全圖形(保留作圖痕跡);
(2)完成下面的證明(說明:括號里填寫推理的依據).
證明:∵![]() 是線段
是線段![]() 的垂直平分線,
的垂直平分線,
∴![]() ______(______)
______(______)
∴![]() .
.
∵![]() (______)
(______)
∴![]() .
.
查看答案和解析>>
科目: 來源: 題型:
【題目】某學校共有六個年級,每個年級 10 個班,每個班約 40 名同學.該校食堂共有 10 個窗口中午所有同學都在食堂用餐.經了解,該校同學年齡分布在 12 歲(含 12 歲)到 18歲(含 18 歲)之間,平均年齡 15 歲.小天、小東兩位同學,為了解全校同學對食堂各窗口餐食的喜愛情況,各自進行了抽樣調查,并記錄了相應同學的年齡,每人調查了 60 名同學,將收集到的數據進行了整理.
小天從初一年級每個班隨機抽取 6 名同學進行調查,繪制統計圖表如下:

小東從全校每個班隨機抽取 1 名同學進行調查,繪制統計圖表如下:

根據以上材料回答問題:
(1)寫出圖 2 中 m 的值 ;
(2)小天、小東兩人中,哪個同學抽樣調查的數據能較好地反映出該校同學對各窗口餐食的喜愛情況,并簡要說明另一名同學調查的不足之處;
(3)為使每個同學在中午盡量吃到自己喜愛的餐食,學校餐食管理部門應為 窗口盡 量多的分配工作人員,理由為 .
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,在平行四邊形 ABCD 中,過點 A 作 AE⊥DC 交 DC 的延長線于點 E,過點 D 作DF // EA 交 BA 的延長線于點 F.
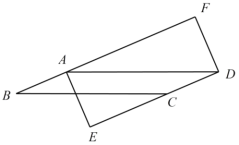
(1)求證:四邊形 AEDF 是矩形;
(2)連接BD,若 AB=AE=2,tan FAD ![]() ,求 BD 的長.
,求 BD 的長.
查看答案和解析>>
科目: 來源: 題型:
【題目】為備戰奧運會,中國女排的姑娘們刻苦訓練,為國爭光,如圖,已知排球場的長度 OD 為 18 米,位于球場中線處球網的高度 AB 為 2.43 米,一隊員站在點 O 處發球,排球從點 O 的正上方 1.8 米的 C 點向正前方飛出,當排球運行至離點 O 的水平距離 OE 為 7 米時,到達最高點 G,建立如圖所示的平面直角坐標系.
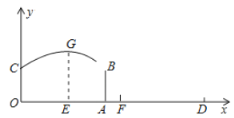
(1)當球上升的最大高度為 3.2 米時,求排球飛行的高度 y(單位:米)與水平距離 x(單位:米)的函數關系式.(不要求寫出自變量 x 的取值范圍)
(2)在(1)的條件下,對方距球網 0.5 米的點 F 處有一隊員,她起跳后的最大高度為 3.1米,問這次她是否可以攔網成功?請通過計算說明.(不考慮排球的大小)
查看答案和解析>>
科目: 來源: 題型:
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 是圓上一點,弦
是圓上一點,弦![]() 于點
于點![]() ,且
,且![]() .過點
.過點![]() 作
作![]() 的切線,過點
的切線,過點![]() 作
作![]() 的平行線,兩直線交于點
的平行線,兩直線交于點![]() ,
,![]() 的延長線交
的延長線交![]() 的延長線于點
的延長線于點![]() .
.

(1)求證:![]() 與
與![]() 相切;
相切;
(2)連接![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com