日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

（1）若從9月到11月使用非智能手機的同學平均增長率相同，那么按此增長率增長到12月份該校使用非智能手機的同學將有多少人？

（2）某于機制造商發現當下市場上售賣的非智能手機大多品質不佳、外觀設計成就，難以滿足市場的需要，所以該廠決定投入12萬元全部用于生產型、型兩款精美的“學生專用手機”投入市場，一部型手機生產成本為400元，售價為600元；一部型手機生產成本為600元，售價為930元，該廠計劃生產型手機的數量不少于型手機數量的2倍，但不超過型手機數量的2.3倍，求生產這批手機并全部售賣后可獲得的最大利潤．

【題目】如圖1，拋物線與軸交于，兩點（點位于點的左側），與軸負半軸交于點，若．

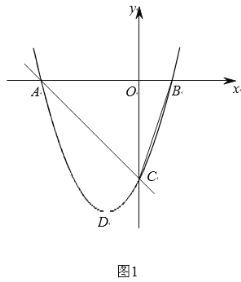
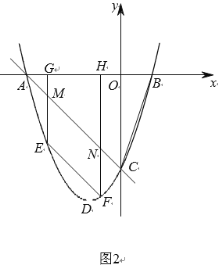
（1）求拋物線的解析式；

（2）如圖2，是第三象限內拋物線上的動點，過點交拋物線于點，過作軸交于點，過作軸交于點，當四邊形的周長最大值時，求點的橫坐標；

（3）在軸下方的拋物線上是否存在一點，使得以、、、為頂點的四邊形被對角線分成面積相等的兩部分．如果存在，求點的坐標；如果不存在，請說明理由．

【題目】我們可以用表示為自變量的函數，如一次函數，可表示，，．

（1）已知二次函數；

①求證：不論為何值，此函數圖像與軸總有兩個交點；

②若，是否存在實數，使得當時，函數的最小值為，若存在，求出的值，若不存在，請說明理由；

（2）已知函數，，若實數、使得，求的值．

【題目】如圖，為的外接圓，，作直線，于．

（1）圖1，求證：是的切線；

（2）圖2，交于點，過點作，垂足為，交于點．

①求證：；

②若，，求的長．

【題目】熊組長準備為我們年級投資1萬元圍一個矩形的運動場地（如圖），其中一邊靠墻，另外三邊選用不同材料建造且三邊的總長為，墻長，平行于墻的邊的費用為200元/，垂直于墻的邊的費用150元/，設平行與墻的邊長為．

（1）若運動場地面積為，求的值；

（2）當運動場地的面積最大時是否會超了預算．

【題目】為監控某條生產線上產品的質量，檢測員每隔相同時間抽取一件產品，并測量其尺寸（），在一天的抽檢結束后，檢測員將測得的各數據按從小到大的順序整理成如下表格：

按照生產標準，產品等級規定如下：

注：在統計優等品個數時，將特等品計算在內；在統計合格個數時，將優等品（含特等品）算在內，

（1）已知此次抽檢的合格率為，請判斷編號為15的產品是否為合格品，并說明理由；

（2）已知此次及抽檢出的優等品尺寸的中位數為．

①__________；

②將這些優等品分成兩組，一組尺寸大于，另一種尺寸不大于，從這兩組中各隨機抽取1件進行復檢，求抽到的2件產品都是特等品的概率．

【題目】(中考·安徽)如圖，已知反比例函數y＝與一次函數y＝k2x＋b的圖象交于A(1，8)，B(－4，m)．

(1)求k1，k2，b的值；

(2)求△AOB的面積；

(3)若M(x1，y1)，N(x2，y2)是反比例函數y＝的圖象上的兩點，且x1<x2，y1<y2，指出點M，N位于哪個象限，并簡要說明理由．

（1）請畫出△A1B1C1，使△A1B1C1與△ABC關于原點對稱；

（2）將△ABC繞點O逆時針旋轉90°，畫出旋轉后得到的△A2B2C2，并直接寫出線段OB旋轉到OB2掃過圖形的面積．

【題目】如圖，點在雙曲線的第一圖像的那一支上，垂直于軸于點，點在軸正半軸上，且，點在線段上，且，點為的中點，若面積為3，則的值為（ ）

A.B.C.D.

(1)若a=-1.

①當函數自變量的取值范圍是-1≤x≤2，且n≥2時，該函數的最大值是8，求n的值;

②當函數自變量的取值范圍是時，設函數圖象在變化過程中最高點的縱坐標為m，求m與n的函數關系式，并寫出n的取值范圍;

（2）若二次函數的圖象還過點A（-2，0），橫、縱坐標都是整數的點叫做整點.已知點，二次函數圖象與直線AB圍城的區域（不含邊界）為T，若區域T內恰有兩個整點，直接寫出a的取值范圍.