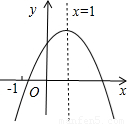相關習題
0 148033 148041 148047 148051 148057 148059 148063 148069 148071 148077 148083 148087 148089 148093 148099 148101 148107 148111 148113 148117 148119 148123 148125 148127 148128 148129 148131 148132 148133 148135 148137 148141 148143 148147 148149 148153 148159 148161 148167 148171 148173 148177 148183 148189 148191 148197 148201 148203 148209 148213 148219 148227 366461
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:填空題
請你寫出一個b的值,使得函數y=x2+2bx在第一象限內y的值隨著x的值增大而增大,則b可以是 .(答案不唯一)
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:填空題
若二次函數的圖象與x沒有交點,且當x≥2時,y隨著x的增大而減小,當x≤2時,y隨著x的增大而增大,請寫出一個符合題意的二次函數解析式 .
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:填空題
對于反比例函數

與二次函數y=x
2-2x-1,請說出它們的兩個相同點:①
,②
;再說出它們的兩個不同點:①
,②
.
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
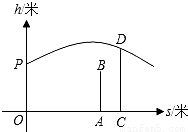
題型:填空題
甲、乙兩人進行羽毛球比賽,甲發出一顆十分關鍵的球,出手點為P,羽毛球飛行的水平距離s(米)與其距地面高度h(米)之間的關系式為h=-
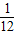
s
2+

s+

.如圖,已知球網AB距原點5米,乙(用線段CD表示)扣球的最大高度為

米,設乙的起跳點C的橫坐標為m,若乙原地起跳,因球的高度高于乙扣球的最大高度而導致接球失敗,則m的取值范圍是
.
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:填空題
已知二次函數y=ax
2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b>m(am+b),(m≠1的實數).
其中正確的結論有
(填序號)
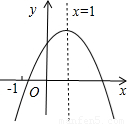
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:解答題
已知函數y=x
2+bx-1的圖象經過點(3,2)
(1)求這個函數的解析式;
(2)畫出它的圖象,并指出圖象的頂點坐標;
(3)當x>0時,求使y≥2的x的取值范圍.
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:解答題
已知二次函數y=-x2+x.
(1)用配方法把該函數化為y=a(x-h)2+k(其中a、h、k都是常數且a≠0)的形式,并指出函數圖象的對稱軸和頂點坐標;
(2)求這個函數圖象與x軸的交點坐標.
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:解答題
二次函數y=ax
2+bx+c(a≠0)的圖象如圖所示,根據圖象解答下列問題:
(1)寫出方程ax
2+bx+c=0的兩個根;
(2)寫出不等式ax
2+bx+c>0的解集;
(3)寫出y隨x的增大而減小的自變量x的取值范圍;
(4)若方程ax
2+bx+c=k有兩個不相等的實數根,求k的取值范圍.

查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:解答題
某校八年級學生小麗、小強和小紅到某超市參加了社會實踐活動,在活動中他們參與了某種水果的銷售工作,已知該水果的進價為8元/千克,下面是他們在活動結束后的對話.
小麗:如果以10元/千克的價格銷售,那么每天可售出300千克.
小強:如果以13元/千克的價格銷售,那么每天可獲取利潤750元.
小紅:通過調查驗證,我發現每天的銷售量y(千克)與銷售單價x(元)之間存在一次函數關系.
(1)求y(千克)與x(元)(x>0)的函數關系式;
(2)設該超市銷售這種水果每天獲取的利潤為W元,那么當銷售單價為何值時,每天可獲得的利潤最大?最大利潤是多少元?【利潤=銷售量×(銷售單價-進價)】
查看答案和解析>>
科目:
來源:《第2章 二次函數》2010年單元總結與測試(解析版)
題型:解答題
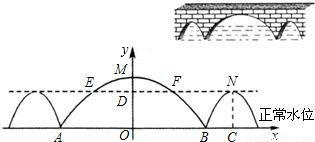
如圖,三孔橋橫截面的三個孔都呈拋物線形,兩小孔形狀、大小都相同.正常水位時,大孔水面寬度AB=20米,頂點M距水面6米(即MO=6米),小孔頂點N距水面4.5米(即NC=4.5米).當水位上漲剛好淹沒小孔時,借助圖中的直角坐標系,求此時大孔的水面寬度EF.
查看答案和解析>>

 與二次函數y=x2-2x-1,請說出它們的兩個相同點:① ,② ;再說出它們的兩個不同點:① ,② .
與二次函數y=x2-2x-1,請說出它們的兩個相同點:① ,② ;再說出它們的兩個不同點:① ,② .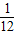 s2+
s2+ s+
s+ .如圖,已知球網AB距原點5米,乙(用線段CD表示)扣球的最大高度為
.如圖,已知球網AB距原點5米,乙(用線段CD表示)扣球的最大高度為 米,設乙的起跳點C的橫坐標為m,若乙原地起跳,因球的高度高于乙扣球的最大高度而導致接球失敗,則m的取值范圍是 .
米,設乙的起跳點C的橫坐標為m,若乙原地起跳,因球的高度高于乙扣球的最大高度而導致接球失敗,則m的取值范圍是 .