
科目: 來源: 題型:
如圖,分別以Rt△ABC的直角邊AC及斜邊AB向外作等邊△ACD、等邊△ABE.已知∠BAC=30º,EF⊥AB,垂足為F,連結DF.

(1)求證:AC=EF;
(2)求證:四邊形ADFE是平行四邊形.
【解析】由等邊△ABE和Rt△ABC,求得Rt△ABC∽Rt△EAF,即可得AC=EF,由等邊三角形的性質得出∠BDF=30°,從而證得△DBF≌△EFA,則AE=DF,再由FE=AB,得出四邊形ADFE為平行四邊形
查看答案和解析>>
科目: 來源: 題型:
在某市舉辦的“讀好書,講禮儀”活動中,東華學校積極行動,各班圖書角的新書、好書不斷增多,除學校購買外,還有師生捐獻的圖書.下面是七年級(1)班全體同學捐獻圖書的情況統計圖:
請你根據以上統計圖中的信息,解答下列問題:

(1)該班有學生多少人?
(2)補全條形統計圖;
(3)七(1)班全體同學所捐獻圖書的中位數和眾數分別是多少?
【解析】(1)根據捐2本的人數是15人,占30%,即可求得總人數;
(2)首先根據總人數和條形統計圖中各部分的人數計算捐4本的人數,進而補全條形統計圖;
(3)根據中位數和眾數的定義解答
查看答案和解析>>
科目: 來源: 題型:
某批發商以每件50元的價格購進800件T恤.第一個月以單價80元銷售,售出了200件;第二個月如果單價不變,預計仍可售出200件,批發商為增加銷售量,決定降價銷售,根據市場調查,單價每降低1元,可多售出10件,但最低單位應高于購進的價格;第二個月結束后,批發商將對剩余的T恤一次性清倉銷售,清倉時單價為40元.設第二個月單價降低x元.
(1)填表(不需要化簡)
| 時間 | 第一個月 | 第二個月 | 清倉時 |
| 單價(元) | 80 | ▲ | 40 |
| 銷售量(件) | 200 | ▲ | ▲ |
(2)如果批發商希望通過銷售這批T恤獲利9000元,那么第二個月的單價應是多少元?
【解析】一元二次方程的運用
查看答案和解析>>
科目: 來源: 題型:
如圖,等腰梯形ABCD中,AD∥BC,AD=AB=CD=2,∠C=60°,M是BC的中點.
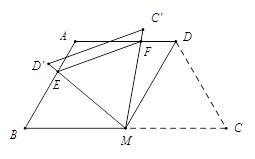
(1)求證:△MDC是等邊三角形;
(2)將△MDC繞點M旋轉,當MD(即MD′)與AB交于一點E,MC(即MC′)同時與AD交于一點F時,點E,F和點A構成△AEF.試探究△AEF的周長是否存在最小值.如果不存在,請說明理由;如果存在,請計算出△AEF周長的最小值.
【解析】此題考核等邊三角形的判定,旋轉的性質
查看答案和解析>>
科目: 來源: 題型:
如圖,已知![]() ,以
,以![]() 為直徑,
為直徑,![]() 為圓心的半圓交
為圓心的半圓交![]() 于點
于點![]() ,點
,點![]() 為弧CF的中點,連接
為弧CF的中點,連接![]() 交
交![]() 于點
于點![]() ,
,![]() 為△ABC的角平分線,且
為△ABC的角平分線,且![]() ,垂足為點
,垂足為點![]() .
.
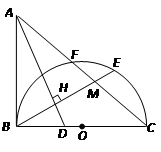
(1)求證:![]() 是半圓
是半圓![]() 的切線;
的切線;
(2)若![]() ,
,![]() ,求
,求![]() 的長.
的長.
【解析】此題考核圓的切線,相似三角形的性質
查看答案和解析>>
科目: 來源: 題型:
已知:如圖1,矩形ABCD中,AB=6,BC=8,E、F、G、H分別是AB、BC、CD、DA四條邊上的點(且不與各邊頂點重合),設m=EF+FG+GH+HE,探索m的取值范圍.
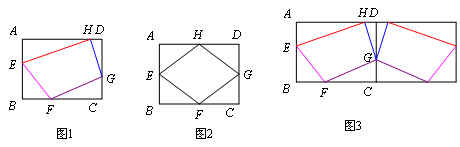
(1)如圖2,當E、F、G、H分別是AB、BC、CD、DA四邊中點時,m=________.
(2)為了解決這個問題,小貝同學采用軸對稱的方法,如圖3,將整個圖形以CD為對稱軸翻折,接著再連續翻折兩次,從而找到解決問題的途徑,求得m的取值范圍.
①請在圖1中補全小貝同學翻折后的圖形;
②m的取值范圍是____________.
【解析】本題主要考查對平行四邊形的性質和判定,全等三角形的性質和判定等知識點的理解和掌握
查看答案和解析>>
科目: 來源: 題型:
已知一元二次方程x2+ax+a-2=0.
(1)求證:不論a為何實數,此方程總有兩個不相等的實數根;
(2)設a<0,當二次函數y=x2+ax+a-2的圖象與x軸的兩個交點的距離為![]() 時,求出此二次函數的解析式;
時,求出此二次函數的解析式;
(3)在(2)的條件下,若此二次函數圖象與x軸交于A、B兩點,在函數圖象上是否存在點P,使得△PAB的面積為![]() ,若存在求出P點坐標,若不存在請說明理由.
,若存在求出P點坐標,若不存在請說明理由.
【解析】(1)判斷上述方程的根的情況,只要看根的判別式△=b2-4ac的值的符號就可以了,(2)根據二次函數圖象與x軸的兩個交點的距離公式解答即可.(3)是二次函數綜合應用問題和三角形的綜合應用
查看答案和解析>>
科目: 來源: 題型:
如圖,在△ABC中,點D是BC上一點,∠B=∠DAC=45°.
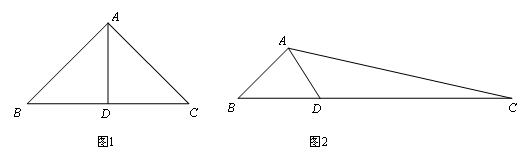
(1)如圖1,當∠C=45°時,請寫出圖中一對相等的線段;_________________
(2)如圖2,若BD=2,BA=![]() ,求AD的長及△ACD的面積.
,求AD的長及△ACD的面積.
【解析】(1)由題意知△ABC、△ABD、△ACD為等腰直角三角形,可求得,(2)利用勾股定理求得AD的長,求得![]() AED
AED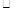
![]() CGD,即可求得△ACD的面積
CGD,即可求得△ACD的面積
查看答案和解析>>
科目: 來源: 題型:
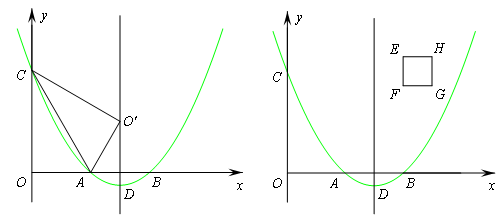
巳知二次函數y=a(x2-6x+8)(a>0)的圖象與x軸分別交于點A、B,與y軸交于點C.點D是拋物線的頂點.
(1)如圖①.連接AC,將△OAC沿直線AC翻折,若點O的對應點0'恰好落在該拋物線的對稱軸上,求實數a的值;
(2)如圖②,在正方形EFGH中,點E、F的坐標分別是(4,4)、(4,3),邊HG位于邊EF的右側.小林同學經過探索后發現了一個正確的命題:“若點P是邊EH或邊HG上的任意一點,則四條線段PA、PB、PC、PD不能與任何一個平行四邊形的四條邊對應相等(即這四條線段不能構成平行四邊形).“若點P是邊EF或邊FG上的任意一點,剛才的結論是否也成立?請你積極探索,并寫出探索過程;
(3)如圖②,當點P在拋物線對稱軸上時,設點P的縱坐標l是大于3的常數,試問:是否存在一個正數a,使得四條線段PA、PB、PC、PD與一個平行四邊形的四條邊對應相等(即這四條線段能構成平行四邊形)?請說明理由.
【解析】二次函數的綜合運用
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com