
【題目】某日,深圳高級中學(集團)南北校區初三學生參加東校區下午![]() 時的交流活動,南校區學生中午
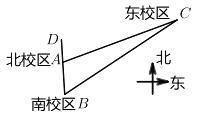
時的交流活動,南校區學生中午![]() 乘坐校車出發,沿正北方向行12公里到達北校區,然后南北校區一同前往東校區(等待時間不計).如圖所示,已知東校區在南校區北偏東
乘坐校車出發,沿正北方向行12公里到達北校區,然后南北校區一同前往東校區(等待時間不計).如圖所示,已知東校區在南校區北偏東![]() 方向,在北校區北偏東
方向,在北校區北偏東![]() 方向.校車行駛狀態的平均速度為
方向.校車行駛狀態的平均速度為![]() ,途中一共經過30個紅綠燈,平均每個紅綠燈等待時間為30秒.
,途中一共經過30個紅綠燈,平均每個紅綠燈等待時間為30秒.
(1)求北校區到東校區![]() 的距離;
的距離;
(2)通過計算,說明南北校區學生能否在![]() 前到達東校區.(本題參考數據:
前到達東校區.(本題參考數據:![]() ,
,![]() )
)
 時刻準備著暑假作業原子能出版社系列答案
時刻準備著暑假作業原子能出版社系列答案 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=6![]() ,BC=3
,BC=3![]() 動點P從點A出發,沿AC以每秒4個單位長度的速度向終點C運動.過點P(不與點A、C重合)作EF⊥AC,交AB或BC于點E,交AD或DC于點F,以EF為邊向右作正方形EFGH設點P的運動時間為t秒.
動點P從點A出發,沿AC以每秒4個單位長度的速度向終點C運動.過點P(不與點A、C重合)作EF⊥AC,交AB或BC于點E,交AD或DC于點F,以EF為邊向右作正方形EFGH設點P的運動時間為t秒.
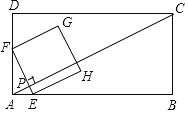
(1)①AC= .②當點F在AD上時,用含t的代數式直接表示線段PF的長 .
(2)當點F與點D重合時,求t的值.
(3)設方形EFGH的周長為l,求l與t之間的函數關系式.
(4)直接寫出對角線AC所在的直線將正方形EFGH分成兩部分圖形的面積比為1:2時t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
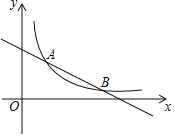
【題目】如圖,已知反比例函數y=![]() (x>0)的圖象與一次函數y=﹣
(x>0)的圖象與一次函數y=﹣![]() x+4的圖象交于A和B(6,n)兩點.
x+4的圖象交于A和B(6,n)兩點.
(1)求k和n的值;
(2)若點C(x,y)也在反比例函數y=![]() (x>0)的圖象上,求當2≤x≤6時,函數值y的取值范圍.
(x>0)的圖象上,求當2≤x≤6時,函數值y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某生產商存有1200千克![]() 產品,生產成本為150元/千克,售價為400元千克.因市場變化,準備低價一次性處理掉部分存貨,所得貨款全部用來生產
產品,生產成本為150元/千克,售價為400元千克.因市場變化,準備低價一次性處理掉部分存貨,所得貨款全部用來生產![]() 產品,
產品,![]() 產品售價為200元/千克.經市場調研發現,
產品售價為200元/千克.經市場調研發現,![]() 產品存貨的處理價格
產品存貨的處理價格![]() (元/千克)與處理數量
(元/千克)與處理數量![]() (千克)滿足一次函數關系(
(千克)滿足一次函數關系(![]() ),且得到表中數據.
),且得到表中數據.
|
|
200 | 350 |
400 | 300 |
(1)請求出處理價格![]() (元千克)與處理數量
(元千克)與處理數量![]() (千克)之間的函數關系;
(千克)之間的函數關系;
(2)若![]() 產品生產成本為100元千克,
產品生產成本為100元千克,![]() 產品處理數量為多少千克時,生產
產品處理數量為多少千克時,生產![]() 產品數量最多,最多是多少?
產品數量最多,最多是多少?
(3)由于改進技術,![]() 產品的生產成本降低到了
產品的生產成本降低到了![]() 元/千克,設全部產品全部售出,所得總利潤為
元/千克,設全部產品全部售出,所得總利潤為![]() (元),若
(元),若![]() 時,滿足
時,滿足![]() 隨
隨![]() 的增大而減小,求
的增大而減小,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
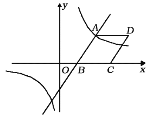
【題目】如圖,已知一次函數![]() 與反比例函數
與反比例函數![]() 的圖象相交于點
的圖象相交于點![]() ,與
,與![]() 軸相交于點
軸相交于點![]() .
.
(1)填空:![]() 的值為 ,
的值為 ,![]() 的值為 ;
的值為 ;
(2)以![]() 為邊作菱形
為邊作菱形![]() ,使點
,使點![]() 在
在![]() 軸正半軸上,點
軸正半軸上,點![]() 在第一象限,求點
在第一象限,求點![]() 的坐標;
的坐標;
查看答案和解析>>
科目:初中數學 來源: 題型:
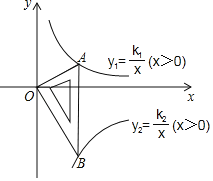
【題目】如圖直角三角板∠ABO=30°,直角項點O位于坐標原點,斜邊AB垂直于x軸,頂點A在函數的y1=![]() 圖象上,頂點B在函數y2=
圖象上,頂點B在函數y2=![]() 的圖象上,則
的圖象上,則![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB=16,O為AB中點,點C在線段OB上(不與點O,B重合),將OC繞點O逆時針旋轉 270°后得到扇形COD,AP,BQ分別切優弧CD于點P,Q,且點P,Q在AB異側,連接OP.
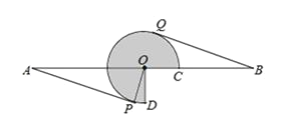
(1)求證:AP=BQ;
(2)當BQ= ![]() 時,求
時,求![]() 的長(結果保留
的長(結果保留 ![]() );
);
(3)若△APO的外心在扇形COD的內部,求OC的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
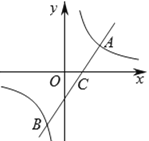
【題目】如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于
的圖象交于![]() ,點
,點![]() 兩點,交
兩點,交![]() 軸于點
軸于點![]() .
.
(1)求![]() 、
、![]() 的值.
的值.
(2)請根據圖象直接寫出不等式![]() 的解集.
的解集.
(3)![]() 軸上是否存在一點
軸上是否存在一點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 三點為頂點的三角形是
三點為頂點的三角形是![]() 為腰的等腰三角形,若存在,請直接寫出符合條件的點
為腰的等腰三角形,若存在,請直接寫出符合條件的點![]() 的坐標,若不存在,請說明理由.
的坐標,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
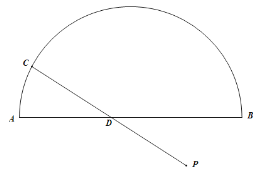
【題目】如圖,![]() 是直徑AB所對的半圓弧,點P是
是直徑AB所對的半圓弧,點P是![]() 與直徑AB所圍成圖形的外部的一個定點,AB=8cm,點C是
與直徑AB所圍成圖形的外部的一個定點,AB=8cm,點C是![]() 上一動點,連接PC交AB于點D.
上一動點,連接PC交AB于點D.
小明根據學習函數的經驗,對線段AD,CD,PD,進行了研究,設A,D兩點間的距離為x cm,C,D兩點間的距離為![]() cm,P,D兩點之間的距離為
cm,P,D兩點之間的距離為![]() cm.
cm.
小明根據學習函數的經驗,分別對函數![]() ,
,![]() 隨自變量x的變化而變化的規律進行了探究.
隨自變量x的變化而變化的規律進行了探究.
下面是小明的探究過程,請補充完整:
(1)按照下表中自變量x的值進行取點、畫圖、測量,分別得到了![]() ,
,![]() 與x的幾組對應值:
與x的幾組對應值:
x/cm | 0.00 | 1.00 | 2.00 | 3.00 | 3.20 | 4.00 | 5.00 | 6.00 | 6.50 | 7.00 | 8.00 |
| 0.00 | 1.04 | 2.09 | 3.11 | 3.30 | 4.00 | 4.41 | 3.46 | 2.50 | 1.53 | 0.00 |
| 6.24 | 5.29 | 4.35 | 3.46 | 3.30 | 2.64 | 2.00 | m | 1.80 | 2.00 | 2.65 |
補充表格;(說明:補全表格時,相關數值保留兩位小數)
(2)在同一平面直角坐標系![]() 中,描出補全后的表中各組數值所對應的點,并畫出函數
中,描出補全后的表中各組數值所對應的點,并畫出函數![]() 的圖象:
的圖象:
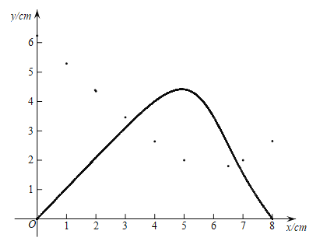
(3)結合函數圖象解決問題:當AD=2PD 時,AD的長度約為___________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com