
如圖所示,在形狀和大小不確定的△ABC中,BC=6,E、F分別是AB.AC的中點,P在EF或EF的延長線上,BP交CE于D,Q在CE上且BQ平分∠CBP,設BP=y,PE=x.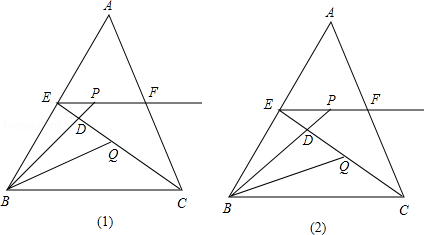
(1)當x= EF時,求S△DPE:S△DBC的值;
EF時,求S△DPE:S△DBC的值;
(2)當CQ= CE時,求y與x之間的函數關系式;
CE時,求y與x之間的函數關系式;
(3)①當CQ= CE時,求y與x之間的函數關系式;
CE時,求y與x之間的函數關系式;
②當CQ= CE(n為不小于2的常數)時,直接寫出y與x之間的函數關系式.
CE(n為不小于2的常數)時,直接寫出y與x之間的函數關系式.
解:(1)∵E、F分別是AB.AC的中點,x= EF,
EF,
∴EF∥BC,且EF= BC,
BC,
∴△EDP∽△CDB,
∴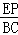 =
= ,
,
∴S△DPE:S△DBC=1:36;
(2)如右圖,設CQ=a,DE=b,BD=c,則DP=y﹣c;
不妨設EQ=kCQ=ka(k>0),則DQ=ka﹣b,CD=(k+1)a﹣b.
過Q點作QM⊥BC于點M,作QN⊥BP于點N,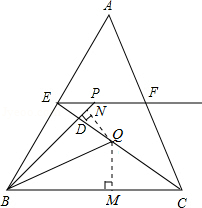
∵BQ平分∠CBP,∴QM=QN.
∴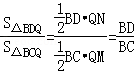 ,
,
又∵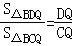 ,
,
∴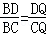 ,即
,即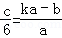 ①
①
∵EP∥BC,∴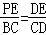 ,即
,即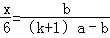 ②
②
∵EP∥BC,∴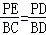 ,即
,即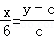 ③
③
由①②③式聯立解得:y=6k﹣x ④
當CQ= CE時,k=1,∴y與x之間的函數關系式為:y=6﹣x.
CE時,k=1,∴y與x之間的函數關系式為:y=6﹣x.
(3)當CQ= CE時,k=2,由(2)中④式可知,y與x之間的函數關系式為:y=12﹣x;
CE時,k=2,由(2)中④式可知,y與x之間的函數關系式為:y=12﹣x;
當CQ= CE(n為不小于2的常數)時,k=n﹣1,由(2)中④式可知,y與x之間的函數關系式為:y=6(n﹣1)﹣x;
CE(n為不小于2的常數)時,k=n﹣1,由(2)中④式可知,y與x之間的函數關系式為:y=6(n﹣1)﹣x;
解析


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
 每年的12月1日是世界艾滋病宣傳日.在一次世界艾滋病大會上,艾滋病病毒感染者和艾滋病病人齊聲呼吁人們的理解,一條長長的紅絲帶(等寬)被拋向會場上空,支持者們將紅絲帶剪成小段,用別針將折疊好的紅絲帶別在胸前.紅絲帶從此成為艾滋病防治的象征,如圖所示.則紅絲帶中重疊部分的形狀是
每年的12月1日是世界艾滋病宣傳日.在一次世界艾滋病大會上,艾滋病病毒感染者和艾滋病病人齊聲呼吁人們的理解,一條長長的紅絲帶(等寬)被拋向會場上空,支持者們將紅絲帶剪成小段,用別針將折疊好的紅絲帶別在胸前.紅絲帶從此成為艾滋病防治的象征,如圖所示.則紅絲帶中重疊部分的形狀是查看答案和解析>>
科目:初中數學 來源: 題型:
 某星期天,小明和他的爸爸開著一輛滿載西瓜的大卡車首次到某古城銷售,來到城門下才發現古城門為拋物線形狀(如圖所示).小明的爸爸把車停在城門外,仔細端詳城門的高和寬以及自己卡車的大小,十分擔心卡車是否能夠順利通過.經詢問得知,城門底部的寬為6米,最高點距離地面5米.如果卡車的高是4米,頂部寬是2.8米,那么卡車能否順利通過?說明理由.(
某星期天,小明和他的爸爸開著一輛滿載西瓜的大卡車首次到某古城銷售,來到城門下才發現古城門為拋物線形狀(如圖所示).小明的爸爸把車停在城門外,仔細端詳城門的高和寬以及自己卡車的大小,十分擔心卡車是否能夠順利通過.經詢問得知,城門底部的寬為6米,最高點距離地面5米.如果卡車的高是4米,頂部寬是2.8米,那么卡車能否順利通過?說明理由.(| 5 |
查看答案和解析>>
科目:初中數學 來源:解題升級 七年級數學 題型:044
如圖A,用力旋轉如圖所示的轉盤A和轉盤B的指針,(1)若想讓指針停在陰影上,那么選哪個轉盤成功的概率比較大?(2)若兩個學生分別轉動轉盤A和轉盤B,轉盤停止后,指針指向幾就順時針走幾格,得到一個數字,如果最終得到的數字是偶數得1分,否則不得分.按以上游戲規則轉動10次轉盤,記錄每次得分結果,得分高為勝,這個游戲對甲、乙兩人公平嗎?說說理由;如果將轉盤A和轉盤B換成如圖B的形狀,該游戲公平嗎?
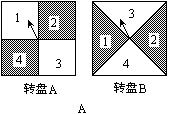

查看答案和解析>>
科目:初中數學 來源:2013屆江蘇無錫市大橋區九年級上學期期末考試數學試卷(帶解析) 題型:解答題
國內某企業生產一種隔熱瓦(其厚度忽略不計),形狀近似為正方形,邊長x(cm)在5~25之間(包括5和25),每片隔熱瓦的成本價(元)與它的面積(cm2)成正比例.出廠價P(元)與它的邊長x(cm)滿足一次函數,圖象如圖所示.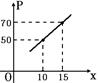
(1)已知出廠一張邊長為15cm的隔熱瓦,獲得的利潤是55元(利潤=出廠價-成本價).
①求每片的隔熱瓦利潤Q(元)與邊長x(cm)之間滿足的函數關系式;
②當邊長為多少時,出廠的隔熱瓦能獲得最大利潤?最大利潤是多少?
(2)在(1)的基礎上,如果廠家繼續擴大產品規模,從5cm~25cm擴大到5cm~60cm.由于20cm~40cm的隔熱瓦屬于國家科技項目,國家對這部分產品進行貼補.每片隔熱瓦貼補W(元)與它的邊長x(cm)滿足: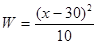 .在推廣20cm~40cm的隔熱瓦時,廠家進行市場營銷,這種規格的隔熱瓦廣告費為每片10元.要使每片隔熱瓦的利潤不低于60.4元,求5cm~60cm的隔熱瓦邊長x的取值范圍(x取整數).
.在推廣20cm~40cm的隔熱瓦時,廠家進行市場營銷,這種規格的隔熱瓦廣告費為每片10元.要使每片隔熱瓦的利潤不低于60.4元,求5cm~60cm的隔熱瓦邊長x的取值范圍(x取整數).
查看答案和解析>>
科目:初中數學 來源:2011-2012學年重慶市九年級3月月考數學試卷(解析版) 題型:解答題
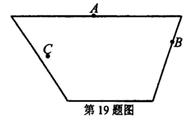
璧山觀音塘濕地公園是目前重慶最大的濕地公園,該公園以眾多珍稀動植物和獨特的燈光和噴泉,吸引著越來越多的游客前往游玩。為了應對游客在游玩過程中的意外傷害,公園決定在形狀為如圖所示的四邊形中央廣場內修建一個便民取藥點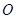 ,以便在里面配置各種應急藥物。現要求該取藥點離兩個廣場入口
,以便在里面配置各種應急藥物。現要求該取藥點離兩個廣場入口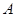 、
、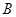 的距離相等,且離觀賞點
的距離相等,且離觀賞點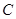 的距離恰好等于
的距離恰好等于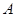 、
、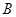 間的距離。請在原圖上利用尺規作圖作出取藥點
間的距離。請在原圖上利用尺規作圖作出取藥點 的位置。(要求:不寫已知、求作、作法和結論,保留作圖痕跡,必須用鉛筆作圖)
的位置。(要求:不寫已知、求作、作法和結論,保留作圖痕跡,必須用鉛筆作圖)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com