
分析 ①根據一元二次方程的定義和判別式的意義得到m2-4≠0且△=(2m+3)2-4(m2-4)≥0,然后求出兩不等式的公共部分即可;
②設方程的兩根為x1、x2,根據根與系數的關系可得出x1+x2=-$\frac{2m+3}{{m}^{2}-4}$、x1•x2=$\frac{1}{{m}^{2}-4}$,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$變形為$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$,代入數據即可得出關于m的分式方程,解方程經檢驗后即可得出結論.
解答 解:①根據題意得m2-4≠0且△=(2m+3)2-4(m2-4)≥0,
解得m≥-$\frac{25}{12}$且m≠±2;
②設方程的兩根為x1、x2,
根據根與系數的關系可得出
x1+x2=-$\frac{2m+3}{{m}^{2}-4}$、x1•x2=$\frac{1}{{m}^{2}-4}$,$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=-2m-3=7,
∴m=-5.
點評 本題考查了一元二次方程ax2+bx+c=0(a≠0)的根的判別式△=b2-4ac:當△>0,方程有兩個不相等的實數根;當△=0,方程有兩個相等的實數根;當△<0,方程沒有實數根.也考查了一元二次方程的定義.


科目:初中數學 來源: 題型:解答題
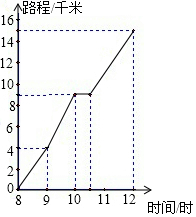 圖為一位旅行者在早晨8時從城市出發到郊外所走的路程與時間的變化圖.根據圖象回答問題:
圖為一位旅行者在早晨8時從城市出發到郊外所走的路程與時間的變化圖.根據圖象回答問題:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com