
分析 (1)原式利用單項式乘除單項式法則計算即可得到結果;
(2)原式括號中兩項通分并利用同分母分式的加法法則計算,同時利用除法法則變形,約分即可得到結果;
(3)原式括號中兩項通分并利用同分母分式的減法法則計算,同時利用除法法則變形,約分得到結果,求出不等式組的整數解確定出x的值,代入計算即可求出值.
解答 解:(1)原式=-8x2y4•$\frac{3x}{4{y}^{6}}$•(-$\frac{6z}{{x}^{2}y}$)=$\frac{36xz}{{y}^{3}}$;
(2)原式=$\frac{a}{a-1}$•$\frac{(a-1)^{2}}{a}$=a-1;
(3)原式=$\frac{-{x}^{2}}{x(x+1)}$•$\frac{(x+1)^{2}}{(x+1)(x-1)}$=-$\frac{x}{x-1}$,
不等式組$\left\{\begin{array}{l}{-x≤1}\\{2x-1<4}\end{array}\right.$,
解得:-1≤x<$\frac{5}{2}$,整數解為-1,0,1,2,
當x=-1,0,1時,原式沒有意義,舍去;
當x=2時,原式=-2.
點評 此題考查了分式的化簡求值,一元一次不等式組的整數解,以及分式的乘除法,熟練掌握運算法則是解本題的關鍵.


 導學與測試系列答案
導學與測試系列答案 新非凡教輔沖刺100分系列答案
新非凡教輔沖刺100分系列答案科目:初中數學 來源: 題型:選擇題
 在“兩學一做”活動中,某社區居民在一幅長90cm,寬40cm的矩形形狀的宣傳畫的四周加上寬度相同的邊框,制成一幅掛圖(如圖),如果宣傳畫的面積占這個掛圖面積的72%,所加邊框的寬度為xcm,則根據題意列出的方程是( )
在“兩學一做”活動中,某社區居民在一幅長90cm,寬40cm的矩形形狀的宣傳畫的四周加上寬度相同的邊框,制成一幅掛圖(如圖),如果宣傳畫的面積占這個掛圖面積的72%,所加邊框的寬度為xcm,則根據題意列出的方程是( )| A. | (90+x)(40+x)=90×40×72% | B. | (90-2x)(40-2x)=90×40×72% | ||
| C. | (90+2x)(40+2x)×72%=90×40 | D. | (90+x)(40+x)×72%=90×40 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
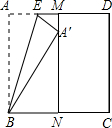 如圖,正方形紙片ABCD的邊長為1,M、N分別是AD、BC邊上的點,且AB∥MN,將紙片的一角沿過點B的直線折疊,使A落在MN上,落點記為A′,折痕交AD于點E,若M是AD邊上距D點最近的n等分點(n≥2,且n為整數),則A′N=$\frac{\sqrt{2n-1}}{n}$.
如圖,正方形紙片ABCD的邊長為1,M、N分別是AD、BC邊上的點,且AB∥MN,將紙片的一角沿過點B的直線折疊,使A落在MN上,落點記為A′,折痕交AD于點E,若M是AD邊上距D點最近的n等分點(n≥2,且n為整數),則A′N=$\frac{\sqrt{2n-1}}{n}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com